- Instabilities: branching, oscillations, cavitation
- Weakly nonlinear theory, crack tip singularity
The ability of solids to withstand mechanical forces is one of their fundamental properties. When a solid is loaded externally, there reaches a point where its global energy can be reduced by breaking into pieces, i.e by creating new free surfaces instead of continuing to store mechanical energy. The major vehicle for these failure processes are cracks, which are non-equilibrium propagating dissipative structures. Cracks are "natural laboratories" for probing material behavior under extreme conditions as their tips concentrate stresses and strains that approach a mathematical singularity. Moreover, crack propagation involves many interacting time and length scales ranging from the linear elastic forcing on large scales to the strong non-linearities and dissipation on the small scales near the crack's tip.
Cracks often exhibit rather complex dynamics, including some poorly understood instabilities, and the laws that govern their motion have remained an object of constant study for nearly a century. My research aims at understanding the origin of crack tip instabilities and the structure of the near tip region. The research combines theoretical tools (classical field theory, asymptotic expansions, perturbation theory, complex analysis, field singularities) and close interaction with experimental work.

The post-mortem crack pattern.
A sequence of photographs of a rapidly propagating crack undergoing a transition from straight (top two pictures) to oscillatory motion, courtesy of A. Livne and J. Fineberg.
See also Phys. Rev. Lett. 98, 124301 (2007).
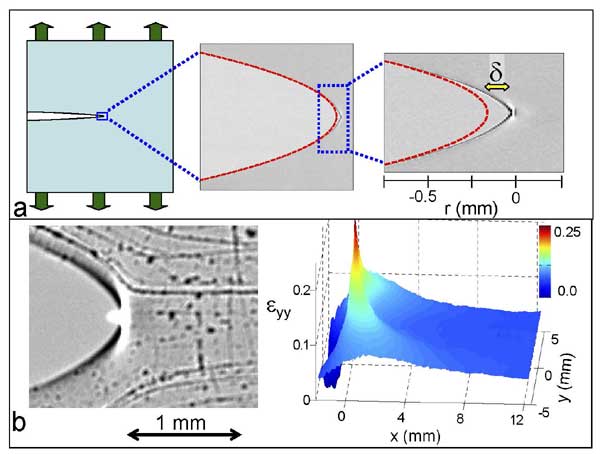
(a) A sketch of a crack propagation experiment (left).
A ~5mm2 close-up on the crack tip region (center). The dashed red line is the parabolic crack tip opening profile predicted by Linear Elastic Fracture Mechanics (LEFM). Zooming in on the crack tip region reveals the existence of a nonlinear zone (deviation from the parabolic profile), whose size is denoted by δ (right).
(b) Blowup of the near-tip region with an imprinted tracer field that allows a direct measurement of the deformation (left). The measured yy-component of the strain field near the tip of the crack (right). The "singular" behavior is apparent. Quantitative analysis of this field confirmed the weakly nonlinear theory of dynamic fracture.
Selected publications
-
Instability in dynamic fracture and the failure of the classical theory of cracks
C. H. Chen, E. Bouchbinder, A. Karma
Nature Physics 13, 1186–1190 (2017) arXiv:1707.03661 -
Failing softly: A fracture theory of highly-deformable materials
T. Goldman Boué, R. Harpaz, J. Fineberg, E. Bouchbinder
Soft Matter 11, 3812-3821 (2015), arXiv 1502.04848 -
The Dynamics of Rapid Fracture: Instabilities, Nonlinearities and Length Scales
E. Bouchbinder, T. Goldman, J. Fineberg
Rep. Prog. Phys. 77, 046501 (2014). arXiv 1305.0989 -
Dynamic stability of crack fronts: Out-of-plane corrugations
M. Adda-Bedia, R. E. Arias, E. Bouchbinder , E. Katzav
Phys. Rev. Lett. 110, 014302 (2013). arXiv:1209.0619 -
A nonlinear symmetry breaking effect in shear cracks
R. Harpaz, E. Bouchbinder
J. Mech. Phys. Solids 60, 1703 (2012). arXiv:1111.2452


