
Between 2006-2010 at the Technion, we have studied coherent optical excitations of atoms in a hot vapor, concentrating on slow and stored light. The main emphasis of the reasearch was the implication of thermal motion on these processes. We investigated diffusion of atomic coherence in structured optical modes, spectral broadening and narrowing mechanisms, optical diffraction manipulation and diffusion of light-matter polaritons, and motional-induced vector potential for light.
The summaries below detail some interesting results. To learn more about this, see our recent review on coherent diffusion of polaritons in atomic media in the Review of Modern Physics (pdf).
Coherent storage of arbitrary patterns in atomic vapor
with Moshe Shuker, Rami Pugatch, Amiram Ron, and Nir Davidson
 |
|
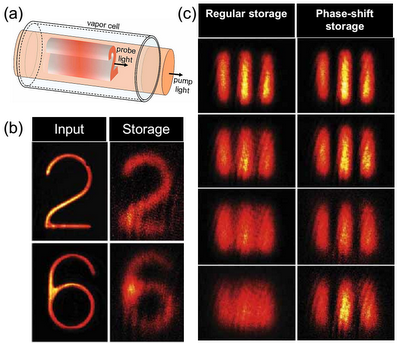
(a) Storing an image of the digit '2' in an EIT medium of room-temperature atoms. (b) The left column shows the original images sent to the cell. The right shows the images after they have been stored and retrieved. The '2' and '6' were stored for 2 and 6 µs, respectively. (c) Storage of an image of three resolution lines (340 µm wide). The left column shows the storage of a constant-phase image for 2, 10, 20, and 30 µs. The right shows the improved resolution achieved when a π phase-shift was applied to the central line, proving that the phase pattern was stored. |
Electromagnetically induced transparency (EIT) is a unique light-matter interaction that can be used to store a light field in the ground-state coherence of a room-temperature atomic ensemble [PRL 86, 783 (2001)]. A 'probe' light pulse, on resonance with the atomic transition, is made to propagate with little absorption in the medium by the aid of a strong 'pump' field. The probe pulse is slowed down and can be stored in the medium by turning off the pump. After a controllable delay, similarly to a hologram, the probe can be retrieved. The storage processes maps the complex amplitude of the light field onto the coherence field (or superposition) of the ground-state atoms. The retrieval fidelity is thus limited by various decay mechanisms of the ground-state coherence. Coherent conversion of information from light to matter and vice versa is considered a cornerstone of quantum information applications. In quantum networks, for example, light may communicate information between nodes, while atomic ensembles store or process the information.
In this work, we have studied how to slow and store arbitrary three-dimensional light fields [PRL 100, 223601 (2008), (pdf)]. In particular, we have demonstrated the storage of a light vortex beam and its topological stability against diffusion [PRL 98, 203601 (2007), (pdf)]. We performed the EIT process in with room-temperature rubidium atoms immersed in neon buffer-gas. While the pump beam was a plane wave, an arbitrary transverse image was imprinted on the probe beam using a binary mask, as illustrated in the figure. After the probe pulse entered the vapor cell, the pump beam was turned off for several microseconds, during which both the amplitude and the phase of the probe’s electric field were encoded on the atoms. The probe field was afterwards retrieved and measured using a CCD camera.
Panel (b) shows two of the images, the digits 2 and 6, as sent to the cell (“input”) and after the storage. The stored images are smoothed, especially near the sharp edges in the originals. We attribute this to diffusion of the atoms during the storage (and also during the slow propagation of the pulse in the EIT vapor). We obtained a quantitative measure of the possible storage resolution by storing an image of three resolution lines, depicted in (c). As the storage duration increases, the effect of the diffusion is more pronounced, and, after 30 µs, the image is completely blurred.
The effect of diffusion can be reduced by exploiting the fact that the phase of the light field is stored together with its intensity. To demonstrate this, we flipped the phase of the central line by π, which in turn flipped the phase of the atomic coherence created in the medium for that line. Therefore, during diffusion, the average coherence in the gaps between the lines was reduced due to destructive interference, and the restored image remained dark in the gaps between the lines, dramatically improving the visibility, as shown in (c), on the right. This method is analogous to an optical technique to reduce the effect of diffraction — phase-shift lithography.
Numerical calculations, based on our analytic theoretical model [PRA 77, 043830 (2008), (pdf)] agree well with the experimental results.
[Adapted from Opt. Photon. News 19, 39 (2008) (pdf)]
Diffraction elimination: Dragging slow light with diffusing atoms
with Paz London, Moshe Shuker, Amiram Ron, and Nir Davidson
 |
| (a) After 50 mm of free-space diffraction, the 100-µm features in the image are substantially distorted. When EIT takes place (Δ=0), the diffracting image is slowed, dragged by the moving atoms, and exhibits diffusion. At Δ<0 however, both the diffraction and the diffusion are eliminated. (b) In an analogy to Doppler cooling of atoms with negative detuning, outwards-confronting light components couple more efficiently to inwards moving atoms, counterbalancing the natural diffraction. (c) The digit '2', otherwise diffracting substantially, is imaged using a negative-diffraction medium in a slab-lens configuration. Rays entering the cell refract to the opposite angle and refract back upon exiting. |
Optical diffraction, a fundamental phenomenon dominating the propagation of light in free space, has stimulated research for centuries, its understanding and manipulation being the cornerstones of optical technology. Diffraction elimination of a single optical mode can be obtained, as in an optical fiber or a wave guide, by patterning the index of refraction in the real transverse plane. However within these wave guides, a multi-mode pattern is not maintained, and arbitrary images rapidly blur out.
In this work, we have realized a medium with novel optical properties, in which the paraxial diffraction is manipulated in its natural wave-vector basis. We experimentally demonstrated several realizations of optical control over the magnitude and orientation of diffraction: non-diffractive propagation of arbitrary images, negative-diffraction lensing, and optically-induced deflection.
We have seen above how images, imprinted on a laser pulse, can be dramatically slowed when traversing an alkali vapor medium via electromagnetically induced transparency (EIT) [PRL 100, 223601 (2008), (pdf)]. Delayed images in vapor have also been performed with weak coherent pulses [PRL 98, 043902 (2007)] and have demonstrated the preservation of quantum coherence and entanglement [Nature 457, 859-862 (2009)].
At a typical group velocity of 1000 m/s, the propagation of slow light is strongly affected by the thermal motion of the room-temperature atoms. Introducing an inert buffer-gas attenuates the ballistic motion and reduces it to the diffusion regime, but nevertheless the diffusion distance of the alkalies might still be comparable to the features size of the propagating image. [In an equivalent spectral interpretation, the frequent collision with the buffer gas atoms cause Dicke narrowing of the Doppler spectrum, and the complex susceptibility becomes quadratic in the transverse momentum space, cf. PRA 77, 043830 (2008), (pdf)]. Thus, on top of the free-space diffraction, slowed images are partially dragged by the atoms and undergo diffusion and additional induced paraxial-diffraction – the magnitude of which is determined by the EIT frequency detuning Δ.
In such a medium, the optical diffraction of slow images can be eliminated completely [Nature Physics 5 665-668 (2009), PRL 102, 043601 (2009) (pdf)], as illustrated in panel (a) of the figure. By setting an appropriate detuning (Δ<0) and carefully tuning the EIT parameters, the induced diffraction completely counterbalances the paraxial free-space diffraction. Somewhat surprisingly, the diffusion can also be canceled in this regime, resulting in a non-diffractive non-diffusive propagation of arbitrary images. As illustrated in panel (b), the random thermal motion of the atoms is exploited to 'Doppler trap' the light in the plane perpendicular to the propagation direction, regardless of its location. No other vapor medium exists that eliminates the optical diffraction of arbitrary images and for any distance throughout their propagation. The sign, magnitude, and direction of the induced diffraction can be optically controlled by varying the EIT parameters. For example, we have demonstrated a regime in which the diffraction occurs twice as fast and the possibility of inflicting a directional bias on a diffracting light beam. Most intriguing, we have realized a medium with a negative diffraction, in which the diffraction behaves as in a negative-index material, see panel (c).
[Adapted from Opt. Photon. News 20,32 (2009) (pdf)]
The elegant modes of coherent diffusion
with Paz London, Dimitry Yankelev, Rami Pugatch, Moshe Shuker and Nir Davidson
 |
| Coherent diffusion expands the Gaussian modes at their waist plane (cell A) in a self-similar manner, as demonstrated for the fundamental Gaussian mode, LG modes of radial order 0 and orbital orders 1 and 2, and an HG mode of Cartesian orders (0,1). Far from the waist (cell B), coherent diffusion results in a contraction. All images are 1.6 × 1.6 mm. |
A light beam in free space always experiences some diffraction, and its cross-section changes throughout the propagation. An imaging lens can then be used to reverse this non-dissipative process. In certain media however, as the one discussed above, the light field also experiences coherent diffusion, which distorts its cross-section irreversibly. The term coherent refers to the fact that the field, carrying amplitude and phase, exhibits destructive and constructive interference when diffusing.
In this work [PRL 105, 183602 (2010), (pdf)], we have studied a family of complex Gaussian modes of coherent diffusion, analogous to those well-known for optical diffraction, by holographically imprinting them on the hot diffusing atoms.
In his renowned book Lasers, A. E. Siegman differentiates between the “standard” and the “elegant” sets of beam-like solutions for the optical diffraction equation. The sets differ in the polynomial profile within the Gaussian cross-section of the beam. The standard solutions, such as the familiar Laguerre- or Hermite- Gaussian modes, maintain their transverse intensity pattern along the optical axis, up to a scaling, while their phase fronts curve or flatten. They are thus self-similar under diffraction. In contrast, the elegant solutions, formulated for being a mathematically “neater alternative set” of solutions, are not self-similar. It can be shown however, that when it comes to coherent diffusion, the standard and elegant solutions exchange roles: The latter evolve in a self-similar manner, corresponding to the modes of coherent diffusion, while the former are distorted.
In our setup, traveling light pulses resonantly interact with a hot alkali gas, and the electromagnetic field can be spatially mapped onto the field of atomic spin coherence using a storage-of-light procedure [PRL 100, 223601 (2008), (pdf)]. During storage, the atoms diffuse, and the resulting field after diffusion can be measured by retrieving and imaging the light pulse. Positioning the beam waist at the center of the vapor cell, we have followed the diffusion of four different modes (cell A in the figure). The self-similar expansion is verified by collapsing the retrieved cross-sections of each mode onto a single profile after the proper scaling and normalization, as predicted by the theory. The waist area increases linearly with time according to the diffusion law, while the dark features in the pattern remain dark. For example, while the vortex of the LG01 mode expands outwards, its dark center does not fill, since atoms diffusing inwards from dipolar points destructively interfere [PRL 98, 203601 (2007), (pdf)].
Perhaps counter-intuitively, coherent diffusion can also cause contraction. Placing the cell beyond the Rayleigh distance (cell B), the rapid phase variations of the diffusing field, due to its curved wave-fronts, result in a contraction of the mode. We have observed this effect for short storage duration, as well as the subsequent expansion, which takes over once the growing Rayleigh distance effectively surpasses our cell.
Coherent diffusion is found in various systems in addition to ours, such as NMR, spintronics, and others. It can be viewed as a complex (dissipative) version of optical diffraction, leading to valuable analogies together with some important differences. In particular, the Gaussian modes of diffusion provide a powerful tool for describing its spatial dynamics.


