Photons, the fundamental particles of light, do not interact with each other in everyday life. Such interactions exist only within 'nonlinear' optical materials and usually require a huge number of photons to be meaningful. In our lab, we realize a medium that pushes nonlinear optics to its extreme (quantum) limit, where the photon-photon interaction is strong on the level of individual photons.
Experiments in Harvard and MIT have demonstrated a "photonic hourglass," through which photons can only pass one-by-one, and a two-photon bound state pertaining to a "photonic molecule". These are decribed in:
- "Quantum nonlinear optics with single photons enabled by strongly interacting atoms", Nature (London) 488, 57-60 (2012)
- "Attractive photons in a quantum nonlinear medium", Nature (London) 502, 71–75 (2013)
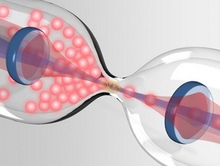
Dissipative photon-photon interaction results in the scattering of photons close together. It thus prevents the transmission of more than one photon at a time for a narrow light-beam. The rate of outgoing photons is independent of the incoming rate and (in our case) saturates at the level of 1 per microsecond, in analogy to an hourglass.
What is quantum nonlinear optics?
Imagine nonlinear optics pushed to the extreme limit of the quantum world, at the sub-picowatt levels. In this regime, the particle-like nature of light becomes significant, and the most basic concepts of optics and photonics need to be reexamined. The Kerr effect, for example, where the light itself alters the refraction index of a medium, can be viewed as a medium-mediated, ‘dispersive’ interaction between the photons. The realization of these interactions between individual photons could make light behave akin to conventional particles, such as electrons and atoms.
Achieving strong interactions between individual photons has been a goal at the forefront of the quantum-optics research for several decades. These interactions constitute a fundamental tool towards the ultimate control of light fields ‘quantum by quantum’. They can be used to realize deterministic two-qubit optical gates for scalable quantum computing and to produce highly-correlated states for high-precision measurements. But perhaps most fascinating, they enable the exploration of new quantum states and phases, similar to those explored in strongly correlated particle systems.
Quantum nonlinear optics (QNLO) refers this new physical regime, where the optical response of a system is not linear already at the level of single photons.
Pinky and the Brain talk about strongly-interacting photons (for non-expert)
QNLO with Rydberg atoms
Current ongoing experiments with atomic gases gradually enter the regime of QNLO by using the atoms to mediate effective interactions between individual photons. The interactions are enabled by coherently coupling the photons to high-lying electronic orbitalsknown as Rydberg states. In our experiment, we have used the n=100 orbital, n being the principal quantum number.
Transitions among Rydberg states have huge electric dipole moments, scaling as n2. The dipolar interaction between two Rydberg atoms can thus become substantial at distances as large as 10 micrometers (for n=100), much larger than the optical wavelength. At these distances, the interaction is of the Van der Walls form and scales as n11 (!). By 'substantial', we mean that the energy shifts due to the Rydberg-Rydberg interaction are larger than the linewidth of the optical excitation, implying dramatic changes to the optical response.
To maintain the nature of the photons while coupling them to Rydberg atoms, we utilize a well-established technique to transform the photons entering the medium into propagating polaritons. Each polariton is a superposition of a photon and an atomic (Rydberg) excitation. These so-called dark-state polaritons exhibit several unique properties: their group velocity is much smaller than the speed of light in vacuum owing to their stationary atomic components; their group-velocity dispersion endows them with an effective mass; and their absorption (scattering) is suppressed despite the light being resonant with the atomic transitions. To learn more about dark-state polaritons, slow light, and the underlying mechanism of electromagnetically-induced transparency, refer to this review or to our page on polariton experiments.
In our experiments, the Rydberg polaritons slow down to about 100 m/s (compared to c=300000 km/s), indicating 99.9999% Rydberg excitation probability. This ensures the ad-hoc excitation of a Rydberg atom per propagating photon. Therefore, individual photons effectively acquire large electric dipoles, long-range interactions, and mass. They traverse the medium as massive polaritons while experiencing strong, long-range interactions.
Several useful concepts have been introduced in the context of coherent Rydberg excitations and interactions. These include the Rydberg blockade, which prevents the excitation of two Rydberg atoms, and the Rydberg macro-atoms, a coherent two-level system comprising many atoms. The following papers review these concepts and their experimental realizations and discuss the implications for quantum information processing and nonlinear optics:
[1] J. D. Pritchard, K. J. Weatherill, and C. S. Adams, Nonlinear optics using cold Rydberg atoms, Annual Review of Cold Atoms and Molecules 1 301-350 (2013). [arxiv]
[2] R. Löw et al. An experimental and theoretical guide to strongly interacting Rydberg gases, J. Phys. B: At. Mol. Opt. Phys. 45 113001 (2012). [arxiv]
[3] M. Saffman, T. G. Walker, and K. Mølmer, Quantum information with Rydberg atoms, Rev. Mod. Phys. 82, 2313–2363 (2010). [arxiv]

Top view of the vacuum chamber in the MIT/Harvard experiment. The atomic cloud is trapped at the intersection of the dipole-trap beams (yellow). Photons from the probe beam (red) transform to polaritons when entering the cloud and transform back when exiting.

Optical non-linearity at the picowatt levels. The transmission through the medium at resonance depends strongly on the density of photons inside the medium.

Two-photon correlation function g(2) in the dissipative regime. The g(2) function measures the probability to detect two photons, normalized to that in a classical laser light. The QNLO medium reduces to 10% the probability that two photons exit the medium simultaneously (“anti-bunching”).
The MIT/Harvard experiment
In a set of recent experiments, we have realized strong quantum non-linearity in a cloud of cold rubidium atoms and observed both dissipative (2012) and dispersive (2013) interactions between individual photons.
In our experimental setup, cold atoms are transferred from a magneto-optical trap (MOT) into a far-detuned optical trap (1064 nm), forming a cloud of length 150 µm and diameter 30 µm at a temperature of 40 µK and peak densities up to 1012/cc. The coupling of ground to Rydberg states includes the probe photons at 780 nm and a strong field at 480 nm. The properties of the interaction between the polaritons are controlled by detuning the optical frequencies from the atomic resonances, while keeping a high (50%) overall transmission.
In the dissipative regime, a single photon propagating in the medium scattered and blocked nearby photons with >90% probability. To achieve such high efficiency, we focused the probe to a waist radius much below 10 µm, ensuring that photons could not propagate side by side. We used single-photon detectors to measure the temporal correlations of the outgoing photons and showed that photons only leave the medium one-by-one, a phenomenon known as anti-bunching.
In the dispersive regime, no photon losses occur due to the interaction, but rather a phase is picked up by the interacting photons. The shift in the two-photon phase with respect to the phase picked up by a single photon is called 'conditional' or 'nonlinear' phase. We demonstrated a conditional phase of 1 radian for two photons, very close to the ultimate value of π required for quantum gates and implying a Kerr effect 100 times stronger than previously obtained. Due to this dynamics, our system produced entangled photon pairs from initially independent photons.
Furthermore, thanks to the effective mass of the polaritons, the distance-dependent phase-shift translates into a mutual force. The evolution of the photonic wave-function resembles the Schrödinger evolution of a massive particle scattering of a finite-range potential. In our case, the force between the polaritons was attractive, and the resulting dynamics was governed by a two-polariton bound state, or 'molecule'. We characterized the wave-function by measuring the correlations of both its amplitude and phase.

In the dispersive regime, the interactions alter the optical phase for two simultaneous photons with respect to single-photon transmission.

Two-photon correlation function g(2) in the dispersive regime (gray circles). The lower effective energy at small distances leads to an attractive force, which bounds photon pairs and gives rise to bunching. The blue line is the solution of an approximated Schrödinger equation, taking into account the effective polariton mass.
What's next?
Studying and engineering QNLO systems could enable realizations of novel many-body physics, applications in light manipulation and metrology, and better photon-by-photon control for information processing. We are interested in studying photonic crystalline and correlated liquid phases, as well as highly entangled states of light. Further theoretical and experimental investigation is required to extend out understanding to time-dependent dynamics and to more than one spatial dimension. Finally, the development of better experimental techniques is important for achieving higher interaction strengths and fidelity, and perhaps for extending the principles learned with cold atoms to other media.



