Research
Review of my Present Research
I’ll start by discussing here my present interests, while offering the possibility to fully review my publications over the years (1961-2011).
My present research interests are much within the physics of mesoscopic, nanoscopic and disordered systems.
Mesoscopic physics is a relatively new branch of condensed-matter physics, of which I have been one of the originators. It is concerned with how the behavior of systems whose size is in between micro- and macroscopic, crosses-over between these two regimes. These systems can be handled and addressed by more-or-less usual macroscopic methods, but their behavior may still be dominated by the unusual effects of quantum mechanics.
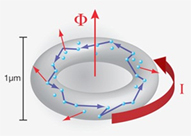
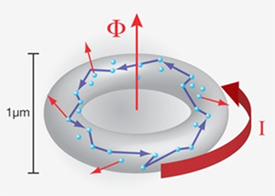Among the interesting new effects found in mesoscopics, there are: the quantization of various conductances, with the universal conductance unit e2/h (with e being the electron’s charge and h Planck’s quantum constant), Aharonov-Bohm (AB) oscillations in the conductance of mesoscopic rings with flux period h/e and "persistent currents" flowing without dissipation in such systems in the normal (non superconducting) resistive state. A nontrivial issue is to explain the magnitude of these currents, on which interesting advances have very recently been made with Ora Entin-Wohlman and our joint student Hamutal Bary-Soroker. This may have to do with fluctuations of mesoscopic superconductivity, which is another exciting subject.
The subject of fluctuations and noise, including the case of systems out of equilibrium, is another direction of my research. I hope to be able to relate some of these results with other recent findings in out-of-equilibrium Physics.
Mesoscopic Physics is very much the forerunner of what is called now “Nanophysics”. The latter is the small size end of the former. A particular example is the problem of so-called “molecular electronics” having to do with the transport of electrons through a molecular bridge between two conducting electrons. Results on the excitation of molecular vibrations by these currents have been and are being obtained with Amnon Aharony and Ora Entin-Wohlman. This problem and several other ones are related with the generic problem of a small system coupled with, or being “observed” by a much larger one, e.g. a reservoir. Relaxation, decoherence and “which path” detection are some of the relevant issues which have reappeared repeatedly in my research.
My research in mesoscopics is strongly coupled with experimental work at the Braun Submicron Center, which, together with Moty Heiblum, I was instrumental in founding. (See http://www.weizmann.ac.il/smc/braun_history.html).
Disordered systems encompass a large variety of real-life examples and my interests have recently been centered on disordered many-electron systems. Of great interest to me is the possible spontaneous formation of inhomogeneous granular-type structures, due to even very weak disorder. This may follow in analogy with a similar formation of domains in, for example, magnetic systems with which I was involved in the past with Shang-keng Ma. Such structures seem to be relevant for many superconducting systems. After settling the issue of superconductivity in a nano-grain, the next issue is the disordered and weakly coupled granular superconductor.
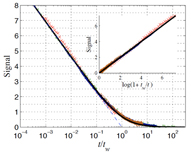
In more heavily disordered systems such as electron glasses, I am currently interested in the slow relaxation and conductance phenomena. Together with Yuval Oreg and our joint student Ariel Amir, we developed recently a model for “electronic glasses” which boasts an interesting, apparently rather universal, spectrum of relaxation rates, λ, going approximately like 1/ λ at small λ. This new universality class of random matrices yields a natural explanation for the ubiquitous logarithmic relaxation of physical quantities in such glasses and for some of the “aging” phenomena, observed in many of them. We believe that this is the beginning of a powerful paradigm for the understanding of such phenomena in glasses. Recently, we have provided an exact solution for the spectrum of an interesting “exponential matrices” model, which does go like 1/ λ at small λ, with small but interesting corrections. This model may well capture much of the relevant physics of quite a few glassy systems. Its success in describing "aging" behavior is demonstrated in the following figure:
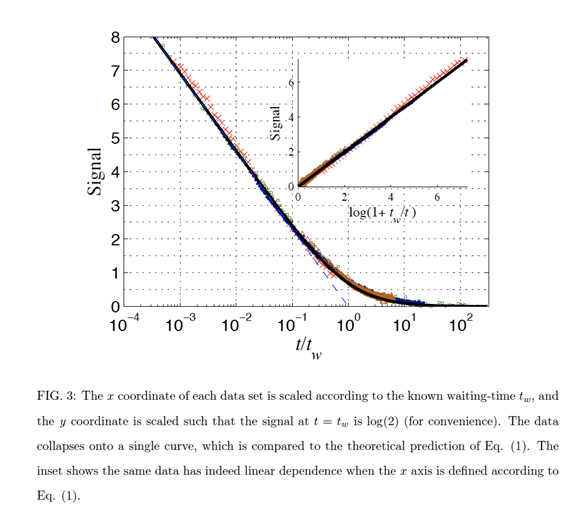
Read further for a more complete review of my research over the years.
