Workshop on Mathematical Physics
Weizmann Institute of Science, January 24-25, 2017
Yosi Avron (Technion)
2016 Nobel prize in physics: D. Thouless and the topology of quantum transport [Presentation] Not Accessible version, For Accessible PDF version contact us
The 2016 Physics Nobel prize was awarded to Thouless and Kosterlitz for the discovery of a new kind of phase transition and to Thouless and Haldane for the discovery of the topological meaning of the Quantum Hall conductance. I shall describe Thouless original finding that the Hall conductance is related to a topological invariant and some of the beautiful mathematical physics that grew from it. No background in condensed matter physics or topology will be assumed.
Roland Bauerschmidt (Cambridge)
Local spectral stability for random regular graphs of fixed degree [Presentation] Not Accessible version, For Accessible PDF version contact us
I will discuss recent results concerning the spectral properties of random regular graphs of large but fixed degree. We prove random matrix type estimates for the delocalisation of the eigenvectors and the concentration of the spectral measure at small scales. Our approach combines the almost deterministic tree-like structure of random regular graphs at small distances with methods from random matrix theory for large distances. This is joint work with J. Huang and H.-T. Yau.
Nick Crawford (Technion)
Stability of the uniqueness phase under non equilibrium perturbations [Presentation] Not Accessible version, For Accessible PDF version contact us
In this talk, I will discuss recent work with W. de Roeck on the following natural question: Given an interacting particle system are the stationary measures of the dynamics stable to small (extensive) perturbations? In general, there is no reason to believe this is so and one must restrict the class of models under consideration in one way or another. As such, I will focus in this talk on the simplest setting for which one might hope to have a rigorous result: attractive Markov dynamics relaxing at an exponential rate to its unique stationary measure in infinite volume. In this case we answer the question affirmatively.
As a consequence we show that ferromagnetic Ising Glauber dynamics is stable to small, non-equilibrium perturbations in the entire uniqueness phase of the inverse temperature/external field plane. It is worth highlighting that this application requires new results on the (exponential) rate of relaxation for Glauber dynamics defined with non-zero external field.
Martin Hairer (Warwick)
Boundary effects for the KPZ equation
There are two ways of defining solution to the KPZ equation with Neumann-type boundary conditions corresponding to "fixing the slope". The first is via the Hopf-Cole transform and the second is by taking limits of smooth approximations. We show that in general these do not coincide. It turns out that the limit of smooth approximations yields a process with a "renormalised" boundary condition that depends on the details of the approximation
Elon Lindenstrauss (Hebrew U.)
Quantum ergodicity on the sphere and averaging operators
The quantum ergodicity theorem of Shnirelman, Colin de Verdiere and Zelditch gives that for an orthonormal sequence of eigenfunctions of the laplacian on a compact manifold with ergodic geodesic flow, outside a density one subsequence, the eigenfunctions equidistribute. The geodesic flow on the sphere is very much not ergodic, and indeed quantum ergodicity (QE) fails on the sphere for the standard sequence of spherical harmonics. On the other hand Zelditch has shown QE holds for a random orthonormal basis in this case. We prove QE for joint eigenfunctions of laplacian and an averaging operator over a finite collection of rotations (with some restrictions). We also give a new approach to a QE theorem on graphs by Anantharaman and Le Masson. Joint work with Shimon Brooks and Etienne Le Masson.
Christophe Sabot (U. Lyons I)
Vertex Reinforced Jump Process, Random Schrodinger Operators, and Hitting Times of Brownian Motions [Presentation] Not Accessible version, For Accessible PDF version contact us
It is well-known that the first hitting time of 0 by a negatively drifted Brownian motion starting at a > 0 has the inverse Gaussian law. Moreover, conditionally on this first hitting time, the BM up to that time has the law of a 3-dimensional Bessel bridge. The Vertex Reinforced Jump Process is a continuous time self-interacting process, closely related to the Edge Reinforced Random Walk. Its behavior can be related to some spectral properties of a random Schrodinger operator with a specific 1-dependent potential. We will explain this and how this random potential also appears as hitting times of a family of interacting drifted Brownian motions, that generalize the classical one-dimensional results mentioned above.
Yinnon Spinka (Tel Aviv U.)
Long-range order in discrete spin systems in high dimensions
Consider a uniformly chosen proper coloring with q colors of a domain in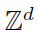 
(i.e.,the zero-temperature anti-ferromagnetic q-state Potts model). It has been known since the work of Dobrushin that if the number of colors is sufficiently large compared with the dimension then the coloring is disordered, having a unique Gibbs state in the thermodynamic limit. We consider an opposite regime, in which the dimension is much higher than the number of colors, and prove that the system admits a staggered (chessboard-like pattern) long-range order, and hence has several translation-invariant Gibbs states. The result extends to the positive-temperature anti-ferromagnetic Potts model as long as the dimension is taken sufficiently high as a function of the temperature. The q = 3 case was previously known. The result further extends to discrete spin systems in which the probability of a configuration is proportional to the product of single-site and nearest-neighbor interactions. The results apply also in low dimensions 
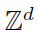if one works with a sufficiently `thickened` version of . Joint work with Ron Peled.
Herbert Spohn (Technische U. Munchen)
KPZ growing interfaces: how flat is flat? [Presentation] Not Accessible version, For Accessible PDF version contact us
In the context of specific model systems I study growing surfaces in one dimension. The initial slopes are assumed to be statistically translation invariant. It is known that for constant initial data the height fluctuations are GOE Tracy-Widom distributed, while for random initial data they are Baik-Rains distributed. In my talk I will discuss the interpolating family of universal distributions.
Eliran Subag (Weizmann)
Geometry and temperature chaos in some spherical spin glasses [Presentation] Not Accessible version, For Accessible PDF version contact us
Spherical spin glasses are smooth Gaussian fields on the N-dimensional sphere. The first part of the talk will deal with recent developments concerning their critical values and a related geometric-probabilistic description for the associated Gibbs measure at low enough temperature, for the pure spherical models and mixed models sufficiently close to pure. While the latter class of models exhibits temperature chaos, the former does not. In the second part of the talk I will explain this, focusing on the qualitative geometric features behind this sharp transition as one moves from pure to mixed models. The talk is based on an ongoing work with Gerard Ben Arous and Ofer Zeitouni.
Li-Cheng Tsai (Columbia)
Criticality of a Randomly Driven Front in One Dimension [Presentation] Not Accessible version, For Accessible PDF version contact us
In this talk we consider a model, in one-dimension, which is a variant of the Modified Diffusion Limited Growth (MDLA), e.g., Kesten, Ramrez, and Sidoravicius, 2012. These models describe an aggregate [0,R (t)] in 
that grows in a bath of random walkers occupying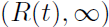 
. In MDLA, the front R (t) of the aggregate moves exactly one step forward whenever a random walker hits the front. In our model, we allow the front to move more steps so that the move matches the number of absorbed particles. Focusing on the critical density 
and the longtime behavior of R (t), in this talk we report a result on the explicit scaling exponent and scaling limit of R (t). The scaling exponent depends on the initial condition, and the scaling limit demonstrates an oscillation between instantaneous super- and sub-critical phases. We will explain the underlying monotonicity and hydrodynamic estimate that leads to the proof of the result. Joint work with Amir Dembo.
