Most proteins act in concert with other proteins, forming permanent or transient complexes. Understanding these interactions at an atomic level is only possible through analysis of protein structures. Over the past few years, there have been efforts to infer the quaternary structures of X-ray crystal structures (Henrick and Thornton 1998; Valdar and Thornton 2001; Ponstingl, Kabir et al. 2003; Bahadur, Chakrabarti et al. 2004), which support the prediction of the Biological Unit to the structure in PDB.
Based on these predictions, we present a visualization and comparison strategy, and construct a hierarchical classification of complexes to integrate and organise the structures. Our strategy is organized in two main steps that we illustrate below:
The representation of proteins complexes as graphs,
The comparison of the graphs.
We also discuss about the symmetry types that are found in protein complexes.
Representing Protein Complexes as Graphs
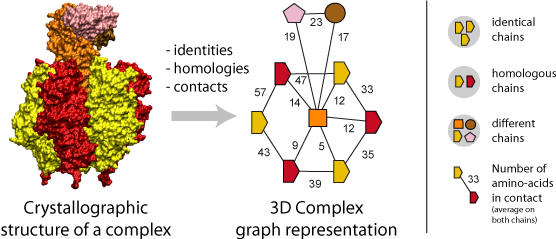
A fundamental step of our method is the translation of each protein complex into a graph. This involves processing the identities, homologies and contacts between the chains within each complex. Structural homology is detected using the N- to C-terminal order of SCOP superfamilies also called the domain architecture, and sequence identity is detected after a FASTA alignment with a 99% sequence identity threshold. Protein-protein interfaces are defined by a threshold of at least ten residues in contact, where the number of residues is the sum contributed by both chains. A residue-residue contact is counted if any pair of atomic groups is closer than the sum of their Van der Waals radii plus 0.5 � (Tsai, Taylor et al. 1999).
The graph itself thus provides the topology of the complex, i.e., the number polypeptides chains (nodes) together with their pattern of interfaces (edges), and an additional label associated to each graph carries the complex symmetry. Also, a label on each edge indicates the number of residues at the interface.
Importantly, the color and shapes of nodes are consistent within a graph but not among different graphs