Relaxation function for a glass-forming system
The movie shows a typical molecular dynamics simulation of a binary mixture of point-particles with Lennard-Jones repulsion (σ/ r)12. `Small' particles have σ=1 and `large' ones have σ=1.4. A relaxation function is made as follows. At time zero every large particle i in the system is assigned a value c i=1 and a neighbour list consisting of its n (small or large) nearest neighbours. In time nearest neighbours wander into the yonder, and when the ith particle loses one (respectively two, three) of its nearest neighbours, having at that time n-1 (respectively n-2, n-3) of the original list, it is assigned a value ci(t)= 2/3, 1/3 and 0 respectively. The relaxation function that we monitor is C(t)≡(2/N)ΣiN ci(t). In the movie any particle for which ci≠ 0 is painted green with intensity of colour proportional to ci(t). The main point to notice is that at longer times only particles that belong to clusters of hexagonal order remain green.

Plastic flow in a glass-forming system
The yellow "center" particle is pulled at a fixed velocity. First the elastic field is being loaded and then a plastic event releases part of the energy stored.

The effect of straining a system in steady-state plastic flow regime
The effect of straining a system which is in its steady-state plastic flow regime. After a short elastic increase in the strain energy the movie shows a plastic event together with an avalanche of subsequent plastic drops in energy.

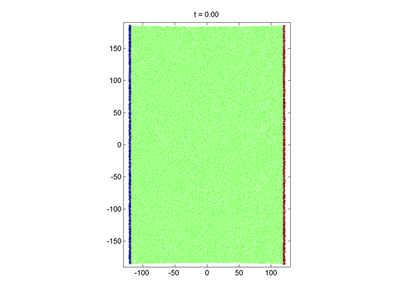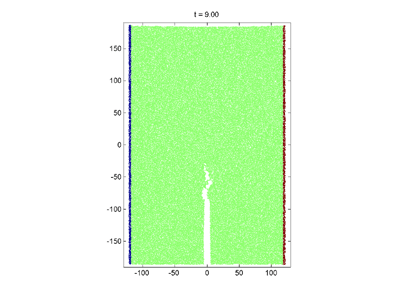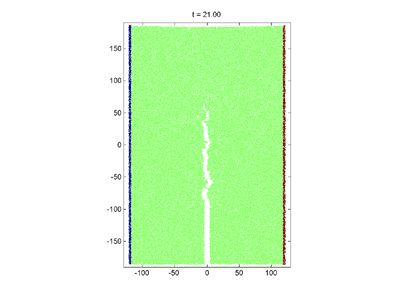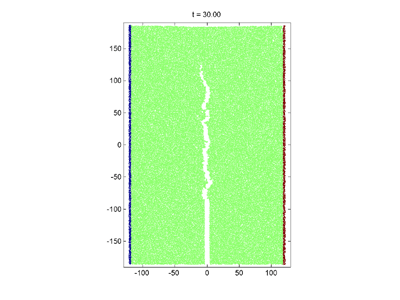
The propagation of a brittle crack under grip boundary conditions
The result of pulling quasi-statically the side boundaries (the particles making up the walls are held frozen). Upper panel: the material is "brittle" and the pulling results in a brittle crack. Lower panel: the material is "ductile" and the pulling induces a plastic flow with a necking instability. Note the large difference in the relative increase in system length compared to the original system size in the two panels. The number of free particles N = 800.

The development of a brittle crack under grip boundary conditions. We were successful in pinpointing the elusive factors influencing a material's brittleness. By using a very short potential cut-off and a deep enough potential well we obtained a material that was brittle enough to sustain a dynamic crack. The finite size effect appears as bending of the upper boundary, releasing the stress before the fracture hits the boundary.
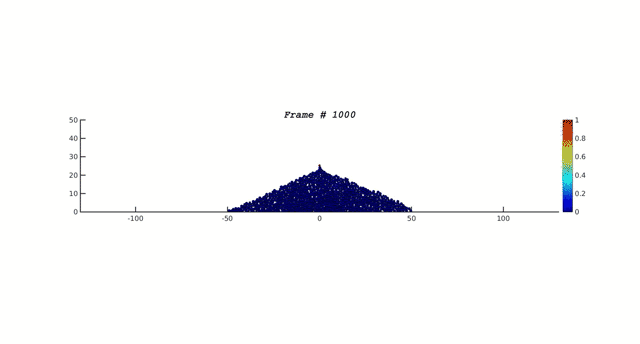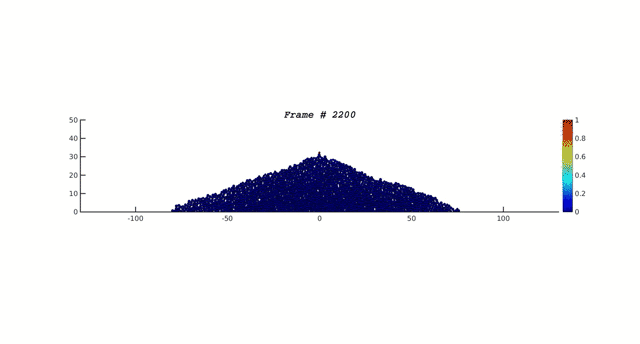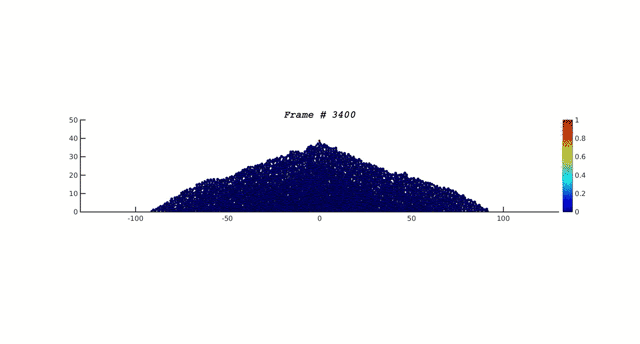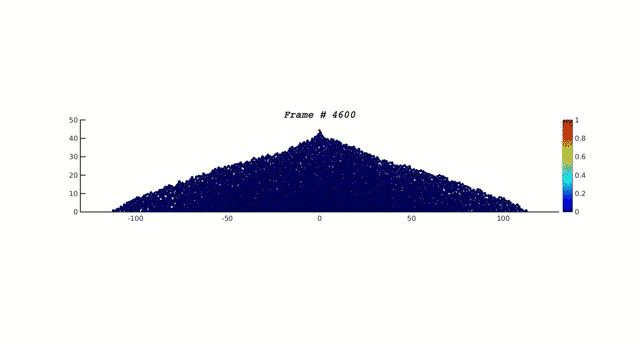
The sandpile revisited
The construction of a sand pile by the addition of smaller and larger particles and allowing the pile to relax to mechanical equilibrium after each addition. The color codes indicates the degree of displacement of particles in the pile during the relaxation to equilibrium. The events show that even deep in the pile there are rearrangements that result in breaking the common assumptions of "frozen" stress field inside the pile. The consequences are explained here.