Pinky and the Brain ponder quantum nonlinear optics

 - Gee, Professor Brain, what are we going to do tonight?
- Gee, Professor Brain, what are we going to do tonight?
 - The same thing we do every night, Researcher Pinky... try to take over the world!
- The same thing we do every night, Researcher Pinky... try to take over the world!
 - How are we going to do that, Brain?
- How are we going to do that, Brain?
 - We shall force two photons to INTERACT, making all the light in the world matter-like…Hoo-Haa!!
- We shall force two photons to INTERACT, making all the light in the world matter-like…Hoo-Haa!!

This also takes 'nonlinear optics' to the extreme limit of the quantum world and thus shall be named QUANTUM NONLINEAR OPTICS.

The crimson balls above symbolize the electric field (distribution) of the two photons, or their spatial wave function. The photons come out at random times from the laser and propagate (to the right) inside a quantum nonlinear optical medium. The interaction between the photons, illustrated by the green lightnings, takes place when the photons are close enough to each other. It could be either a dissipative interaction, causing scattering or absorption of the photons, or a dispersive interaction, conserving the number of photons and inducing phase shifts and forces between them.
 - Professor Brain, may I remind you that the direct interaction between photons requires extremely high energies?
- Professor Brain, may I remind you that the direct interaction between photons requires extremely high energies?  - I appreciate your concerns, Pinky. Obviously we will use matter, namely atoms, to mediate the interaction. For example, we can make one of the photons excite an atom, which in turn prevents the second photon from exciting it, thus making the photons effectively interact!
- I appreciate your concerns, Pinky. Obviously we will use matter, namely atoms, to mediate the interaction. For example, we can make one of the photons excite an atom, which in turn prevents the second photon from exciting it, thus making the photons effectively interact!
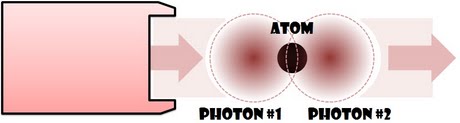
 - But the probability for a single photon to excite a single atom is usually super-ultra small.
- But the probability for a single photon to excite a single atom is usually super-ultra small. - So, we'd crank it up:
- So, we'd crank it up:
- We shall use narrow-band lasers and strong atomic resonances
- We will focus the light to strengthen the electric field of each individual photon
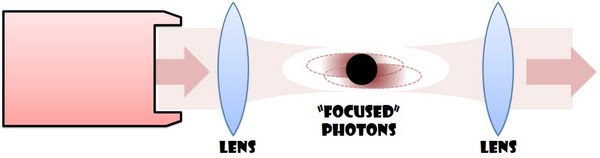
 - Mmm… it seems like the excitation probability is still only a few percent.
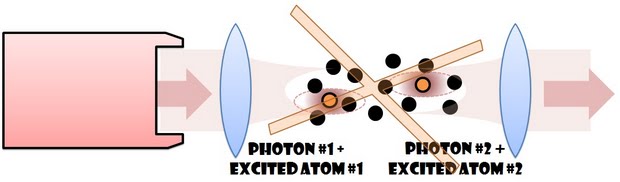
- Mmm… it seems like the excitation probability is still only a few percent. - Then we shall use MORE ATOMS (as illustrated below)!
- Then we shall use MORE ATOMS (as illustrated below)! - WRONG, Brain. Adding atoms to the medium is very helpful for LINEAR processes but much less for NONLINEAR processes. The probability that a single photon excites one of these many atoms can indeed be made high, but this does not guarantee that two photons couple to the SAME atom, and so does not guarantee an interaction between the photons.
- WRONG, Brain. Adding atoms to the medium is very helpful for LINEAR processes but much less for NONLINEAR processes. The probability that a single photon excites one of these many atoms can indeed be made high, but this does not guarantee that two photons couple to the SAME atom, and so does not guarantee an interaction between the photons.
 - Pinky, are you pondering what I'm pondering?
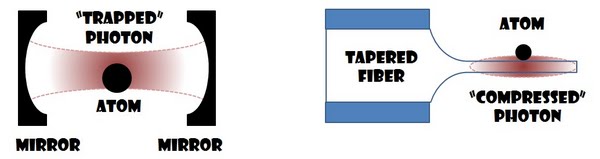
- Pinky, are you pondering what I'm pondering? - Uh, I think so, Brain. We could confine the photons along the beam’s direction using optical CAVITIES (as illustrated on the left below). Generally speaking, multiple reflections of the photons in the presence of the atom could allow for many interaction "opportunities".
- Uh, I think so, Brain. We could confine the photons along the beam’s direction using optical CAVITIES (as illustrated on the left below). Generally speaking, multiple reflections of the photons in the presence of the atom could allow for many interaction "opportunities". - This is the realm of cavity QED and is indeed a very promising approach, attempted in many places in the world.
- This is the realm of cavity QED and is indeed a very promising approach, attempted in many places in the world. - How about confining the photons transversely using SUB-WAVELENGTH structures (as illustrated on the right)? It could substantially increase the electric field per-photon.
- How about confining the photons transversely using SUB-WAVELENGTH structures (as illustrated on the right)? It could substantially increase the electric field per-photon. - That's another successful approach, especially when combined with cavities. It is, too, studied by many groups, including fascinating achievements with microwave photons in super-conducting circuits.
- That's another successful approach, especially when combined with cavities. It is, too, studied by many groups, including fascinating achievements with microwave photons in super-conducting circuits.
 - So what is your plan, Brain?
- So what is your plan, Brain? - None of the above, Pinky. In our approach, we require no confining structures; our photons are essentially free to propagate in all three dimensions. "Where we're going, we don't need roads."
- None of the above, Pinky. In our approach, we require no confining structures; our photons are essentially free to propagate in all three dimensions. "Where we're going, we don't need roads."
In our approach, to circumvent the weak coupling of the photon to a single atom, we do not restrict ourselves to ONE atom mediating the photon-photon interaction. Instead, we let the photons excite DIFFERENT atoms. These excited atoms interact with each other, and via their coupling to the photons induce an effective photon-photon interaction.
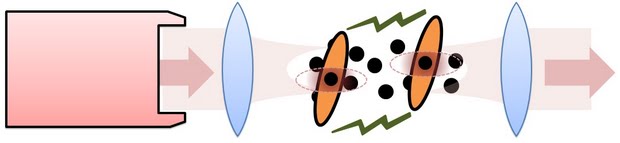
 - Hey, you never mentioned anything about the atoms themselves interacting. And over such long distances. How does this happen?
- Hey, you never mentioned anything about the atoms themselves interacting. And over such long distances. How does this happen? - We choose to excite the atoms to very high electronic levels, known as Rydberg states. In a Rydberg state, one of the electrons orbits the atom very far from the nucleus. For example, at the 100th electronic level (n=100), the orbit's diameter is half a micrometers, 1000 times larger than a ground-state orbit.
- We choose to excite the atoms to very high electronic levels, known as Rydberg states. In a Rydberg state, one of the electrons orbits the atom very far from the nucleus. For example, at the 100th electronic level (n=100), the orbit's diameter is half a micrometers, 1000 times larger than a ground-state orbit. - So the excited atoms effectively act as antennas?
- So the excited atoms effectively act as antennas? - Yes. The electric dipole induced in the Rydberg states is so large, that the interaction between two Rydberg atoms (at n=100) is 1012 times stronger than that of non-excited atoms. They thus interact substantially at distanced as large as 10 micrometers (R in the figure below).
- Yes. The electric dipole induced in the Rydberg states is so large, that the interaction between two Rydberg atoms (at n=100) is 1012 times stronger than that of non-excited atoms. They thus interact substantially at distanced as large as 10 micrometers (R in the figure below).
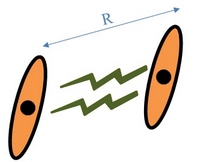
 - So the only thing left for us is to make sure (1) that each photon excites a Rydberg atom, (2) that this excitation travels "with" the photon when it propagates in the medium, and (3) that when the Rydberg atoms interact, the coupling to the photons is sensitive enough to inflict this interaction on the photon. Easy!
- So the only thing left for us is to make sure (1) that each photon excites a Rydberg atom, (2) that this excitation travels "with" the photon when it propagates in the medium, and (3) that when the Rydberg atoms interact, the coupling to the photons is sensitive enough to inflict this interaction on the photon. Easy! - Really?
- Really? - Mmm, yes. This is exactly what happens with slow-light polaritons (and these polaritons were our plan to take over the world last night). Using the slow-light technique, photons slowly propagate in the medium while exciting Rydberg atoms. Such a hybrid light-matter excitation is known as a polariton. These polaritons then strongly interact via the Rydberg-Rydberg interaction!
- Mmm, yes. This is exactly what happens with slow-light polaritons (and these polaritons were our plan to take over the world last night). Using the slow-light technique, photons slowly propagate in the medium while exciting Rydberg atoms. Such a hybrid light-matter excitation is known as a polariton. These polaritons then strongly interact via the Rydberg-Rydberg interaction!

 - Great, so now how do we proceed? how does it look in the lab? what do we observe? what is it good for? Click here to get back to reality ...or take a comic break with this:
- Great, so now how do we proceed? how does it look in the lab? what do we observe? what is it good for? Click here to get back to reality ...or take a comic break with this:
My word, man, don't you know your quantum statistics?!


