Research
We study the "finger-prints" of classical chaos in quantum mechanics. The subjects which interested us most during the past few years were:
|
Correlations between periodic orbit and in the spectra of their actions |
Magnetic edge-states and the duality of the interior and the exterior energy spectra |
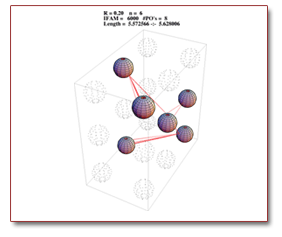 Correlated periodic orbits for the 3-D Sinai billiard Correlated periodic orbits for the 3-D Sinai billiard |
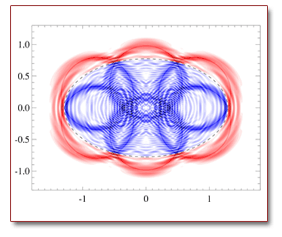 Interior and exterior wave functions for a magnetic ellipse billiard. The wave-functions concentrate along dual classical trajectories in the interior (red) and exterior (blue) Interior and exterior wave functions for a magnetic ellipse billiard. The wave-functions concentrate along dual classical trajectories in the interior (red) and exterior (blue) |
|
Quantum Graphs |
The nodal set of chatoic wave-functions, counting nodal domains, random waves |
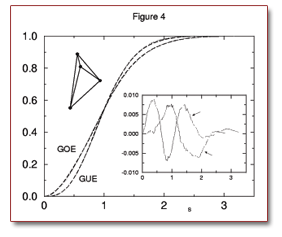 The nearest-neighbor statistics for the spectrum of a connected 4-vertices graph (tetrahedron). This numerical simulation was the starting point for our work on quantum graphs The nearest-neighbor statistics for the spectrum of a connected 4-vertices graph (tetrahedron). This numerical simulation was the starting point for our work on quantum graphs |
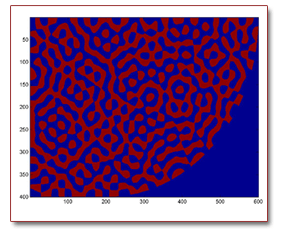 The nodal structure of a typical high lying eigenfunction in a chaotic stadium (billiard) The nodal structure of a typical high lying eigenfunction in a chaotic stadium (billiard) |


