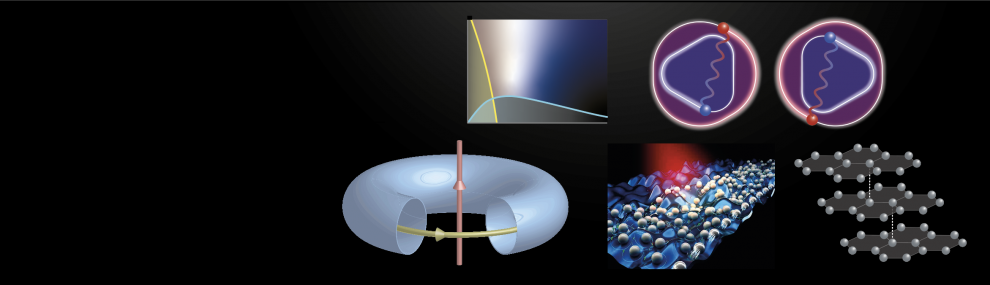
Topology has been recognized as an important principle to characterized phases of quantum matter, from quantum Hall states to topological superconductor. Surprisingly, subjecting the system to a periodicially modulated driving allows for an even richer structure, including non-equliibrium "phases" that are not accessible in static systems. These include new types of anomalous Floquet band structures, non-adiabatic quantized charge pumps, and new types of protected Majorana bound states that may be useful as building blocks for topological qubits.
Selected publications:
-
"Stability of Floquet Majorana box qubits", Anne Matthies, Jinhong Park, Erez Berg, Achim Rosch, arXiv:2110.05281; Accepted to Phys. Rev. Lett. (2022).
- "Topologically protected braiding in a single wire using Floquet Majorana modes", Bela Bauer, T. Pereg-Barnea, Torsten Karzig, Maria-Theresa Rieder, Gil Refael, Erez Berg, and Yuval Oreg, Phys. Rev. B 100, 041102(R) (2019).
- "Universal Chiral Quasisteady States in Periodically Driven Many-Body Systems", Netanel H. Lindner, Erez Berg, and Mark S. Rudner, Phys. Rev. X 7, 011018 (2017).
- "Anomalous Floquet-Anderson Insulator as a Nonadiabatic Quantized Charge Pump", Paraj Titum, Erez Berg, Mark S. Rudner, Gil Refael, and Netanel H. Lindner, Phys. Rev. X 6, 021013 (2016).
- "Anomalous Edge States and the Bulk-Edge Correspondence for Periodically Driven Two-Dimensional Systems", Mark S. Rudner, Netanel H. Lindner, Erez Berg, and Michael Levin, Phys. Rev. X 3, 031005 (2013).
- "Topological characterization of periodically driven quantum systems", Takuya Kitagawa, Erez Berg, Mark Rudner, and Eugene Demler, Phys. Rev. B 82, 235114 (2010).