Research

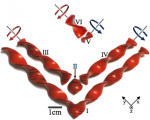
Orientation dependent handedness

From the distinct left handedness of amino acids to the right handedness of a household screw, chiral phenomena pervade of our lives. Yet despite its prevalence and importance the quantitative treatment of handedness is still lacking. Relying on the physicist’s interpretation of the right hand rule as a relation between directions and rotations leads to an orientation dependent quantification through handedness pseudo-tensors.
We construct and study the properties of such handedness pseudo-tensors. We are particularly interested in using these quantities to understand handed self-assembly processes, and to describe handed hydrodynamic flows.

Geometrically frustrated structures

When manufacturing Lego pieces or the pieces of a jigsaw puzzle special care is taken to assure that the pieces would snugly fit next to one another without any need to deform. However, when tissue grows, a ductile material plastically deforms or a microstructure self-assembles there is no similar mechanism to assure that the different constituents would indeed perfectly fit next to one another. The misfit of the different part of the object gives rise to geometric frustation. We are interested in understanding the equilibrium configurations such frustrated object assume. These configurations compromise between the objects' contradicting intrinsic tendencies and gives rise to highly complex structure and exotic response properties.

Geometry is everywhere. Nonetheless, we are mostly oblivious of subtle geometric considerations and notions of geometric non-linearity or geometric frustration. In some cases, however, only an accurate geometric treatment shows a problem's true nature. We welcome such problems wherever they emerge; From colon surgery to the mechanical response of nano scrolls to manoeuvres of nematods.