Irreversible plastic deformation

The ability of solids to deform irreversibly, i.e. plastically, is of enormous importance to human kind. Yet, we have a rather limited fundamental understanding of the physics of plastic deformation in amorphous and heavily dislocated solids. The ultimate theoretical challenge in these fields is to develop dynamic equations of motion - the analog of the Navier Stokes equations - for amorphous and heavily dislocated solids. Building on advances in understanding amorphous materials, through detailed experiments and computer simulations, we have recently extended the original Shear-Transformation-Zones (STZ) theory to conform with the internal-variable, effective-temperature non-equilibrium thermodynamics discussed above. Furthermore, we have recently explored the implications of this thermodynamic framework to strain hardening theory of heavily dislocated polycrystalline solids.

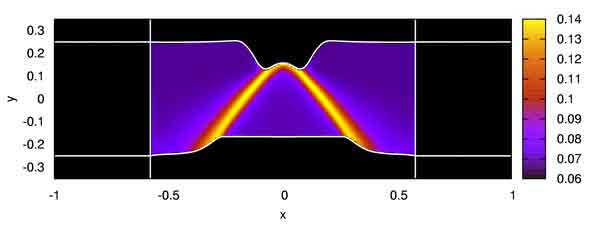
A level set simulation of a continuously deformed bar undergoing a necking instability, using the Shear- Transformation-Zones (STZ) theory. The color code represents the magnitude of the effective temperature that quantifies the degree of local structural disorder. The emergence of shear bands prior to failure is evident.

Figure courtesy of Chris Rycroft, Harvard University.

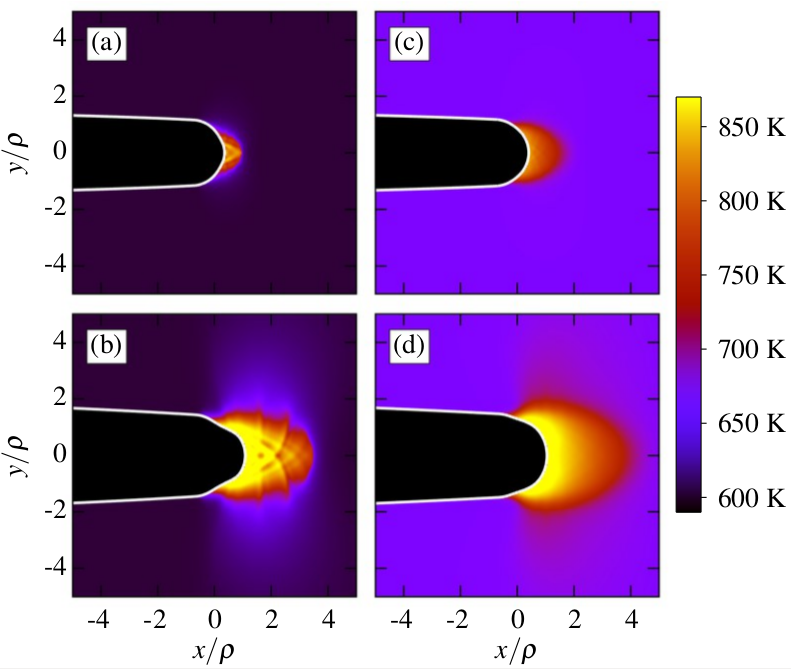
A comparison between the spatial distributions of disorder, quantified by an effective configurational temperature, near the tip of a loaded crack notch in a more structurally-relaxed glass (left panels) and a less structurally-relaxed glass (right panels). A localization process, leading to reduced notch toughness is clearly observed on the left.

The theoretical results allow to understand an experimentally observed an annealing-induced ductile-to-brittle type of transition in bulk metallic glasses.

Selected publications