Driven by Curvature: Cell Shapes and Cell Migration
Cells in our body have a multitude of shapes, according to their function. The factors that determine the local and global shape of a cell, are numerous, including the internal state of the cell, with respect to the cell cycle and metabolism, and the properties of the extracellular matrix (ECM). Cells that are round while floating in solution, change their shapes dramatically when in contact with a solid substrate.
Cells also dynamically change their shapes, growing protrusions of various shapes (filopodia, microvilli, stereocilia), and exhibit propagating waves. The driving forces for all of these phenomena arise in the cytoskeleton, which deforms the membrane that envelopes the cell. We have been developing theoretical models which propose that a unifying mechanism behind many of these cellular shapes is the coupling of the cytoskeleton to the membrane via curved (or curvature-sensitive) elements at the membrane. We demonstrate that this general mechanism can give rise to both protrusions (Turing instability) and propagating waves (Wave instability).
It is still an open question what are the possible shapes and dynamics which can be driven by the curvature-based coupling of the membrane and the cytoskeleton. There are many open puzzles regarding cellular shapes, which remain unsolved.
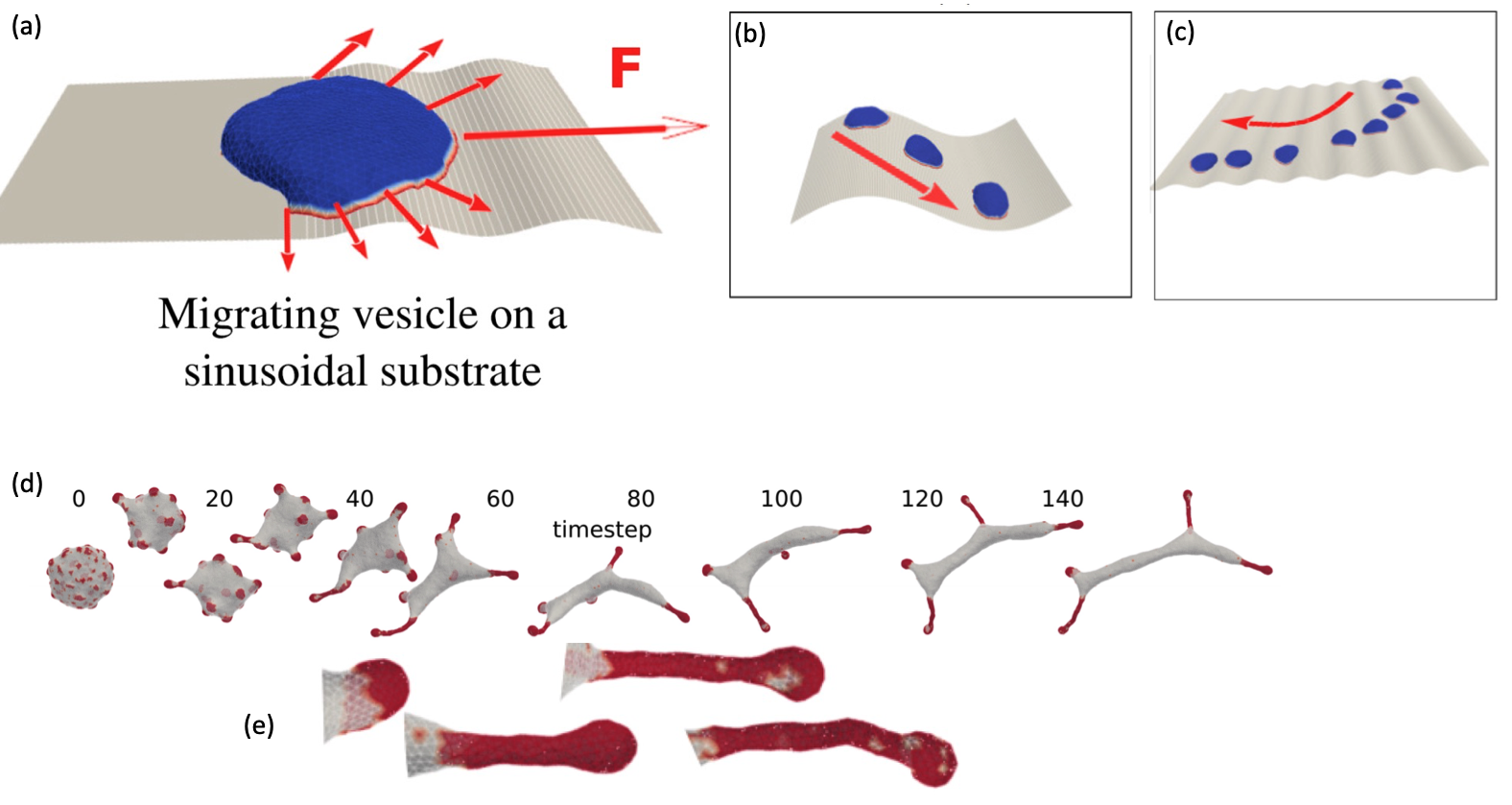
(b) The mini-cell avoids ridges and moves in the grooves, as real cells do.
(c) The mini-cell moves perpendicular to the undulations, when its bigger than the pattern’s wavelength. Cells behave in this way.
(d) The dynamics of the aggregation of curved aligned-force proteins to form elongated, finger-like protrusions (e). These are observed in cells, and play essential roles, such as in neuronal development.
[a-c] R. K. Sadhu et al., A Minimal Physical Model for Curvotaxis Driven by Curved Protein Complexes at the Cell’s Leading Edge, Proc. Natl. Acad. Sci. U.S.A. 121, (2024).
[d-e] Y. Ravid, S. Penič, Y. Mimori-Kiyosue, S. Suetsugu, A. Iglič, and N. S. Gov, Theoretical Model of Membrane Protrusions Driven by Curved Active Proteins, Front. Mol. Biosci. 10, (2023).
Related papers:
- R. K. Sadhu et al., A Minimal Physical Model for Curvotaxis Driven by Curved Protein Complexes at the Cell’s Leading Edge, Proc. Natl. Acad. Sci. U.S.A. 121, (2024). DOI: 10.1073/pnas.2306818121
- Y. Ravid, S. Penič, Y. Mimori-Kiyosue, S. Suetsugu, A. Iglič, and N. S. Gov, Theoretical Model of Membrane Protrusions Driven by Curved Active Proteins, Front. Mol. Biosci. 10, (2023). DOI: 10.3389/fmolb.2023.1153420
- R. K. Sadhu, A. Iglič, and N. S. Gov, A Minimal Cell Model for Lamellipodia-Based Cellular Dynamics and Migration, Journal of Cell Science 136, (2023). DOI: 10.1242/jcs.260744
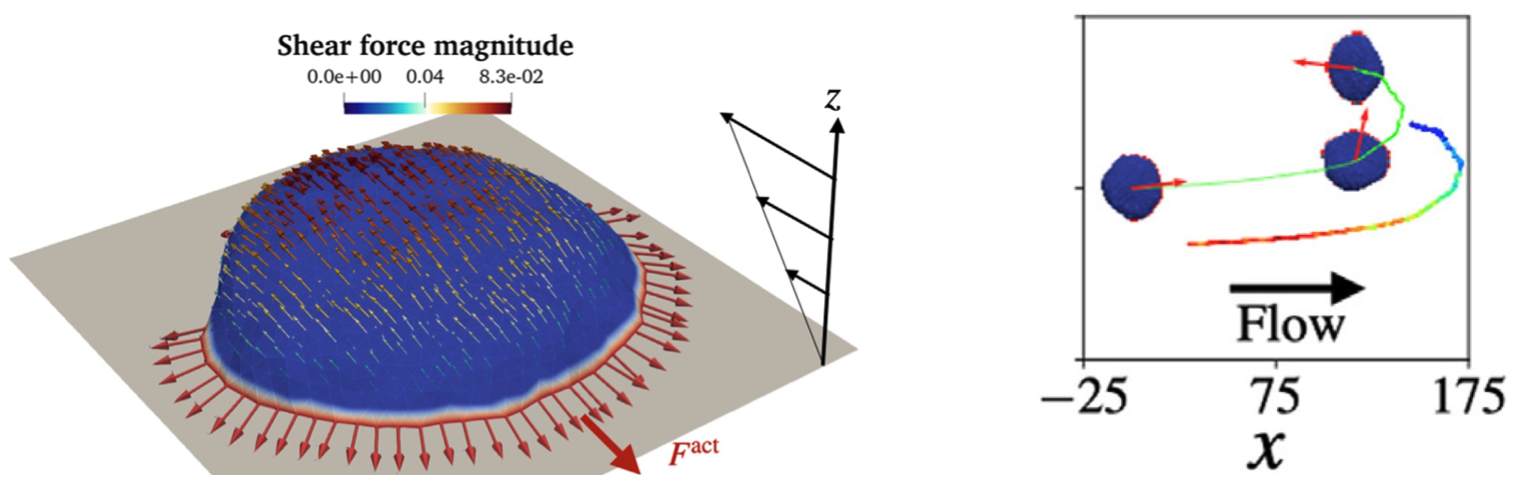
- S. Sadhukhan, S. Penič, A. Iglič, and N. S. Gov, Modelling How Curved Active Proteins and Shear Flow Pattern Cellular Shape and Motility, Front. Cell Dev. Biol. 11, (2023). DOI: 10.3389/fcell.2023.1193793
- R. K. Sadhu, S. R. Barger, S. Penič, A. Iglič, M. Krendel, N. C. Gauthier, and N. S. Gov, A Theoretical Model of Efficient Phagocytosis Driven by Curved Membrane Proteins and Active Cytoskeleton Forces, Soft Matter 19, 31 (2023). DOI: 10.1039/D2SM01152B
- R. K. Sadhu et al., Experimental and Theoretical Model for the Origin of Coiling of Cellular Protrusions around Fibers, Nat Commun 14, (2023). DOI: 10.1038/s41467-023-41273-y
- R. K. Sadhu, S. Penič, A. Iglič, and N. S. Gov, Modelling Cellular Spreading and Emergence of Motility in the Presence of Curved Membrane Proteins and Active Cytoskeleton Forces, Eur. Phys. J. Plus 136, (2021). DOI: 10.1140/epjp/s13360-021-01433-9
- M. Fošnarič, S. Penič, A. Iglič, V. Kralj-Iglič, M. Drab, and N. S. Gov, Theoretical Study of Vesicle Shapes Driven by Coupling Curved Proteins and Active Cytoskeletal Forces, Soft Matter 15, 5319 (2019). DOI: 10.1039/C8SM02356E
