Research

Anomalous Thermal Relaxations

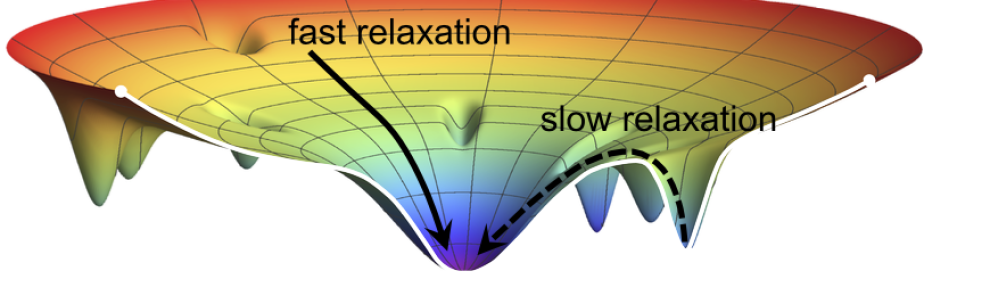
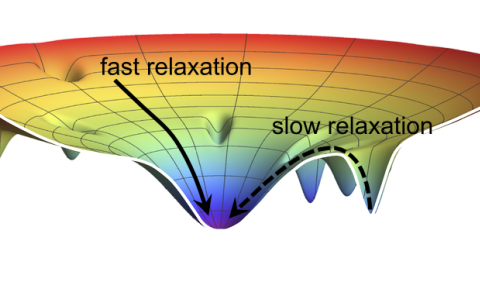
Consider two systems, identical in all macroscopic parameters except their temperatures. When both are coupled to the same environment with a different temperature (say colder or hotter than both systems), which system takes a shorter time to relax to the temperature of the environment? Surprisingly, the relaxation time is not always monotonic with the initial temperature: in some cases the initially hot system cools faster than the initially cold one, or the initially cold system heats faster than the initially hot one. These are examples of ``anomalous relaxation processes", which are not well understood yet.

Periodically Driven Systems

Stanislav Ulam used to say that “…nonlinear science is like referring to the bulk of zoology as the study of non-elephant animals.” On the same token, classifying a system as in or out of equilibrium is not more informative than classifying a location as in-Yehupitz or out-of-Yehupitz.

One specific class of out of equilibrium states that my group is trying to understand is Periodically Driven Systems. In these systems some parameters (temperature, pressure, chemical potential or anything else) are periodically changing with time, and this is the only thing that drives the system out of equilibrium. In other words - once the periodic change is stopped and the parameters are fixed the system relaxes to a geniun thermal equilibrium.

Physics of Computing

Today, almost every physicist use a computer. But all computers are implemented by devices that are based on some physical principles. We explore this interplay between computation and physics.