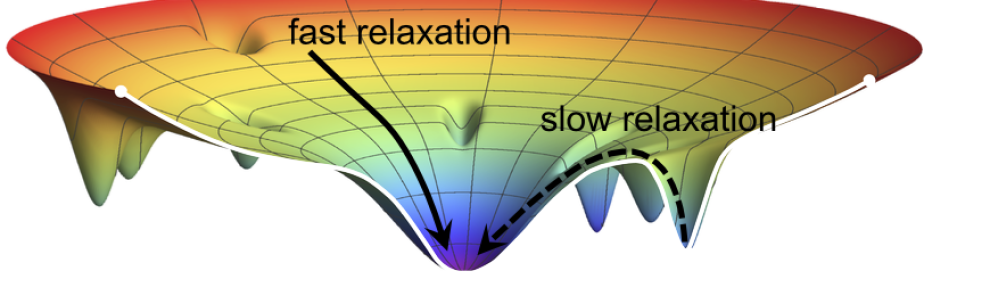
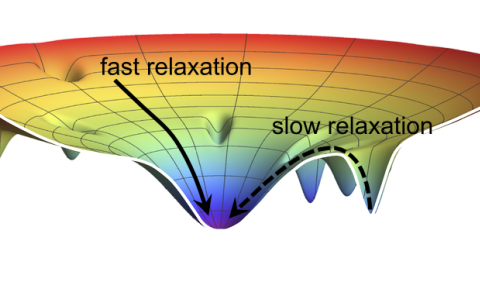
Any computation, regardless of how abstract and complicated it is, must eventually be implemented on some physical system - be it our brain, a silicon based computer, a quantum device or anything else. This implies that the lows of physics set bounds on computations. For example, the ``quantum speed limit" provides a bound on how fast can a basic logical operation be performed, and the Landauer principle sets a minimal limit on the heat dissipated in the process of erasing a bit. However, for most cases our current technology is quite far from these limits, and the actual limiting factors are not universal, but rather technology dependent.
My group is interested in the physics of computation, both as a fundamental concept as well as some specific applications.
We have works on the Landauer limit:
Some of our works are related to coupled lasers as a possible computation devise:
-
Rapid laser solver for the phase retrieval problem (Science Advances 2019)
-
Exact mapping between a laser network loss rate and the classical XY Hamiltonian by laser loss control (Nanophotonics 2020)
-
Anyonic Parity-Time Symmetric Laser (Science Advances 2022)
And recently we are playing with the D-Wave quantum annealer: