Turbulence in non-integer dimensions by fractal Fourier decimation.
Uriel Frisch, Anna Pomyalov, Itamar Procaccia, and Samriddhi Sankar Ray,
Phys. Rev. Lett. 108, 074501 (2012) ArXiv: arXiv:1108.1295
In theoretical physics a number of results have been obtained by extending the dimension d of space from directly relevant values such as 1, 2, 3 to noninteger values. The main difficulty in carrying out such an extension for hydrodynamics in d<2. is to ensure the conservation of energy and enstrophy.
We discovered a new way of fractal decimation in Fourier space, appropriate for hydrodynamics. Fractal decimation reduces the effective dimensionality D of a flow by keeping only a (randomly chosen) set of Fourier modes whose number in a ball of radius k is proportional to kD for large k. At the critical dimension Dc=4/3 there is an equilibrium Gibbs state with a k-5/3 spectrum, as in V. L'vov et al., Phys. Rev. Lett. 89, 064501 (2002).
Spectral simulations of fractally decimated two-dimensional turbulence show that the inverse cascade persists below D=2 with a rapidly rising Kolmogorov constant, likely to diverge as (D-Dc)-2/3 .
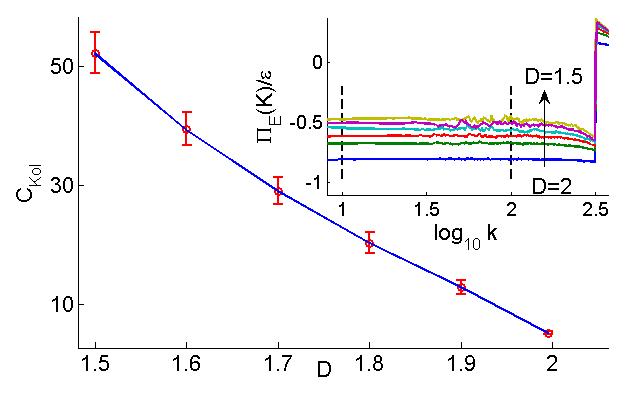
Dependence of the Kolmogorov constant on D. The lowest value, at D= 2, is about 5. The inset shows the energy flux normalized by the energy injection ε.


