Minimal quantum heat machines: We have introduced the minimal and simplest thermal machines in the quantum domain. These may be conceived as (Figure 1) quantized (harmonic-oscillator) 'piston' that couples to a single qubit acting as either a quantum heat engine (QHE) or quantum refrigerator (QR) on spectrally non-flat baths.
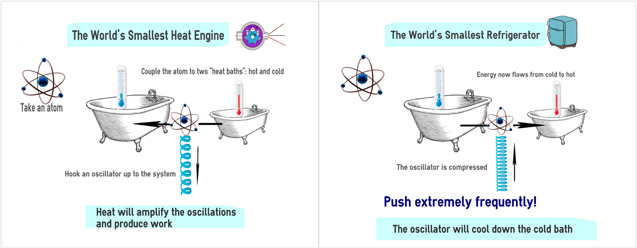
Fig 1. Cartoon of the 'world's simplest and smallest' universal heat machine acting as heat engine (left) or refrigerator (right). It is comprised of a qubit that constantly interacts with two baths at different temperatures. Concurrently, it is driven by an oscillator that off resonantly modulates (by periodic Stark shifts) the qubit resonance frequency. The modulation rate determines whether the qubit will act as a heat engines or refrigerator.
We have shown that a periodically-modulated control qubit coupled to both baths is a minimal model for QHE and QR (Figure 2). It is remarkable that such a simple model allows for both QHE and QR actions.
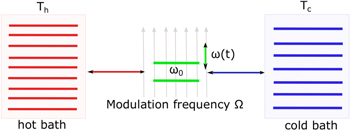
Fig 2. Components of the universal heat machine depicted in figure2: (1) working fluid (qubit system); (2) two baths at different (hot and cold) temperatures, permanently coupled to the qubit (via weak coupling); (3) a piston (external field oscillator) that periodically modulates the qubit (level distance), i.e. ω(t)
Our selected publications on these issues:
Gelbwaser-Klimovsky, D; Alicki, R; Kurizki, G (2013). Minimal Universal Quantum Heat Machine. Physical Review E. 87
Gelbwaser-Klimovsky, D; Alicki, R; Kurizki, G (2013). Work and Energy Gain of Heat-Pumped Quantized Amplifiers. EPL. 103
A.Ghosh et al., Two-level masers as heat-to-work converters, Proc. Nat. Acad. Sci. 115, 9941 (2018)
Nonlinear Coherent Heat Machines: We have changed the paradigm of thermodynamics whereby heat machines are open systems dissipated by heat baths. We have stepped beyond this paradigm by introducing closed-system heat machines that operate in a purely coherent fashion by mixing few hot and cold thermal field modes in interferometers with nonlinear intermode cross-couplers (Fig.3). The simplest example is a four mode interferometer with cross-Kerr couplers with two hot and two cold inputs which sends energy preferentially to a preselected output mode (Fig.3). This is an automatic (autonomous) Maxwell demon that creates a temperature difference between the hot modes, dumping the acquired information as a waste heat into the cold modes. This machine works in a coherent manner, being fully reversible.
Our selected publications on these issues:
T. Opatrny et al. Science Advances, 9, 1070 (2023)
Do quantum effects modify thermodynamic laws? We have explored the impact of quantum effects on performance bounds of heat machines imposed by the laws of thermodynamics:
Thermodynamic equilibrium (Zeroth Law): can be modified by quantum observations.
Energy conservation (First Law): modified by time-energy uncertainty.
Carnot efficiency bound (Second Law): can be exceeded only if the energy comes from a non-thermal bath.
Unattainability of absolute zero (Third Law: can be violated in certain quantum systems.
Thermodynamic equilibrium and energy conservation modification by quantum obervation: The standard, straightforward way of cooling or heating a quantum system is by equilibrating it with a bath at a desired temperature. But can one cool or heat a quantum system while in contact with a bath at a constant temperature? The answer is affirmative!
We have experimentally and theoretically demonstrated (with L Frydman's group at WIS) the possibility of heating or cooling a qubit coupled to a spin bath, by means of repeated non-selective (unread) measurements. We have shown (Figure 4) that the qubit may be cooled down to a temperature that may be much lower than that of the bath by means of a suitable measurement rate that conforms to the condition for the anti-Zeno effect (AZE). By contrast, a measurement rate that corresponds to the quantum Zeno effect (QZE) heats the qubit (see Dynamical Decoherence Control). Hence, temperature can be changed by quantum observations!
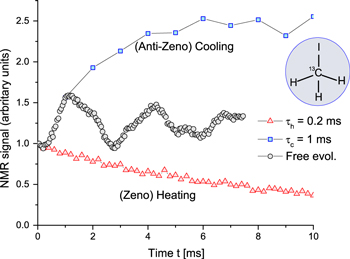
Fig 5. Experimental verification of Zeno heating for QND polarization measurements (at intervals τ=0.2 ms) and anti-Zeno cooling (at intervals τ=1 ms). Experimental setup: quantum system embodied by the nuclear spin of a carbon atom C is in contact with a bath embodied by the nuclear spins of 3 protons. Their off-resonant frequency mismatch is changed by the measurements, causing polarization decrease (heating) or increase (cooling) of C depending on the interval τ.
Our selected publications on these issues:
Erez, N; Gordon, G; Nest, M; Kurizki, G (2008). Thermodynamic Control by Frequent Quantum Measurements. Nature. 452:724-727
GA Alvarez, DDB Rao, L.Frydman and G. Kurizki, Zeno and anti-Zeno polarization control of spin ensembles by induced dephasing, Phys. Rev. Lett. 105, 160401 (2010).
G. Gordon, DDB Rao and G. Kurizki, Equilibration by Quantum Observation, New J. Phys. 12, 053033 (2010).
Beyond Carnot – universal thermodynamic bound on quantum engine efficiency: The efficiency of heat engines is limited by the Carnot bound, attained when the engine cycle is reversible. Quantum engines fuelled by non-thermal (e.g., squeezed-thermal) baths have been shown to surpass this bound. Yet, their maximum efficiency cannot be determined by the reversibility condition, which may yield an unachievable efficiency bound above 1. This prompts the question: What does really limit the efficiency? We identify the fraction of the exchanged energy between a quantum system and a bath that necessarily causes an entropy change and derive a new inequality for the latter. This formulation reveals a universal efficiency bound for quantum engines which does not imply reversibility, unless the baths are thermal. This bound cannot be solely deduced from the laws of thermodynamics. We illustrate these results for the practically-relevant Carnot- and Otto cycles energised by non-thermal baths, which are both shown to be restricted by our new efficiency bound.
Our selected publications on these issues:
W. Niedenzu, V. Mukherjee, A. Ghosh, A.G. Kofman and G. Kurizki, Quantum engine efficiency bound beyond the second law of thermodynamics, Nature Communications 9, 1 (2018).
A.Ghosh, CL Latune, L. Davidovich and G. Kurizki, Catalysis of heat-to-work conversion in quantum machines, Proc. Nat. Acad. Sci. 114, 12156 (2017).
Third-law violation?: To probe the validity of the third law of thermodynamics by Nernst that prohibits the attainability of zero temperature in finite time, we explore the use of a single driven qubit simultaneously coupled to hot and cold spectrally non-flat baths. The possibility of cooling a bath down to arbitrarily low temperatures, i.e. cooling rate scaling with temperature, is thus a fundamental issue that reflects on the applicability of the third law. We assume that the QR pumps heat into an infinite hot bath, and out of a cold bath. Strikingly, we show that arbitrarily low temperature may be reached at finite time (non-exponentially fast) by the heat pump, for an appropriate (magnon) cold-bath spectrum thereby challenging the third law.
Our selected publications on these issues:
Gelbwaser-Klimovsky, D; Niedenzu, W; Kurizki, G (2015). Thermodynamics of Quantum Systems Under Dynamical Control. Advances in Atomic, Molecular, and Optical Physics, Vol 64. 64:329-407.
Kolar, M; Gelbwaser-Klimovsky, D; Alicki, R; Kurizki, G (2012). Quantum Bath Refrigeration Towards Absolute Zero: Challenging the Unattainability Principle. Physical Review Letters.109: 090601.

