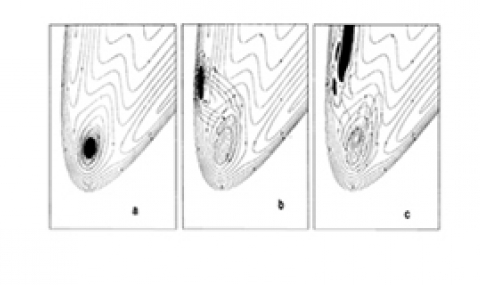
. In the last few years the Tannor group has developed a method to solve both the time-independent and time-dependent Schrödinger equations based on the von Neumann (vN) lattice of phase space Gaussians. By incorporating periodic boundary conditions into the vN lattice they have overcome a longstanding problem of convergence of the vN method. This opens the door to tailoring quantum calculations to the underlying classical phase space structure while retaining the accuracy of the Fourier grid basis. Formally the method defeats exponential scaling with dimensionality. In the classical limit the method reaches the remarkable efficiency of 1 converged eigenstate per 1 basis functions. They have used the method to calculate the vibrational eigenstates of a polyatomic with 104 bound states and to simulate attosecond one-electron and two-electron dynamics in the presence of combined strong XUV and NIR laser fields. The method also has applications to signal and image processing.
Simulation of two-electron attosecond double ionization dynamics in the presence of combined strong XUV and NIR laser pulses.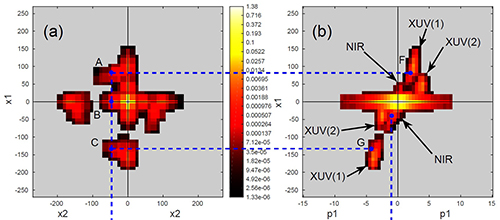
References:
-
A. Shimshovitz and D. J. Tannor, Phase Space Approach to Solving the Time-independent Schrödinger Equation, Phys. Rev. Lett. 109, 070402 (2012).
- N. Takemoto, A. Shimshovitz and D. J. Tannor, Phase Space Approach to Solving the Time-dependent Schrödinger Equation: Application to the Simulation and Control of Attosecond Electron Dynamics in the Presence of a Strong Laser Field, J. Chem. Phys. 137, 011102 (2012) (Communication).
- A. Shimshovitz and D. J. Tannor, Phase Space Wavelets for Solving Coulomb Problems, J. Chem. Phys. 137, 101103 (2012) (Communication).
- E. Assemat, S. Machnes and D. J. Tannor, Double ionization of helium from a phase space perspective, quant-phys arXiv:1502.05165.
- A. Shimshovitz and D. J. Tannor, Periodic Gabor Functions with Biorthogonal Exchange: A Highly Accurate and Efficient Method for Signal Compression, arXiv:1207.0632.