Recent progress in the development of experimental quantum computing devices is on the verge of accomplishing what seemed near-impossible only a decade ago: the engineering of devices that, due to their sheer size — from a few dozen to hundreds of qubits — can no longer be directly classically simulated! This situation has brought the field face to face with a fundamental challenge: given that the quantum device’s behavior cannot be classically predicted — how can it be benchmarked, and can its computation be trusted?
As a motivating example, consider the timely problem of developing tests of quantumness: given access to an experimental device, what kind of test can be performed on it that conclusively establishes that the device has a “non-classical behavior?” Here by “given access to” we refer to the means by which the user (often referred to as the verifier) interacts with the device: by providing classical inputs (instructions) and obtaining classical outputs (measurement outcomes). By non-classical behavior we mean that the input-output behavior that is observed from the device is not one that could be reproduced by a classical computer. Because every
input-output behavior can at least in principle be classically simulated, a test of quantumness necessary relies on some assumption on the device: for example, that it runs in polynomial time, or that it consists of two isolated components each of which the user, or verifier, may interact with.
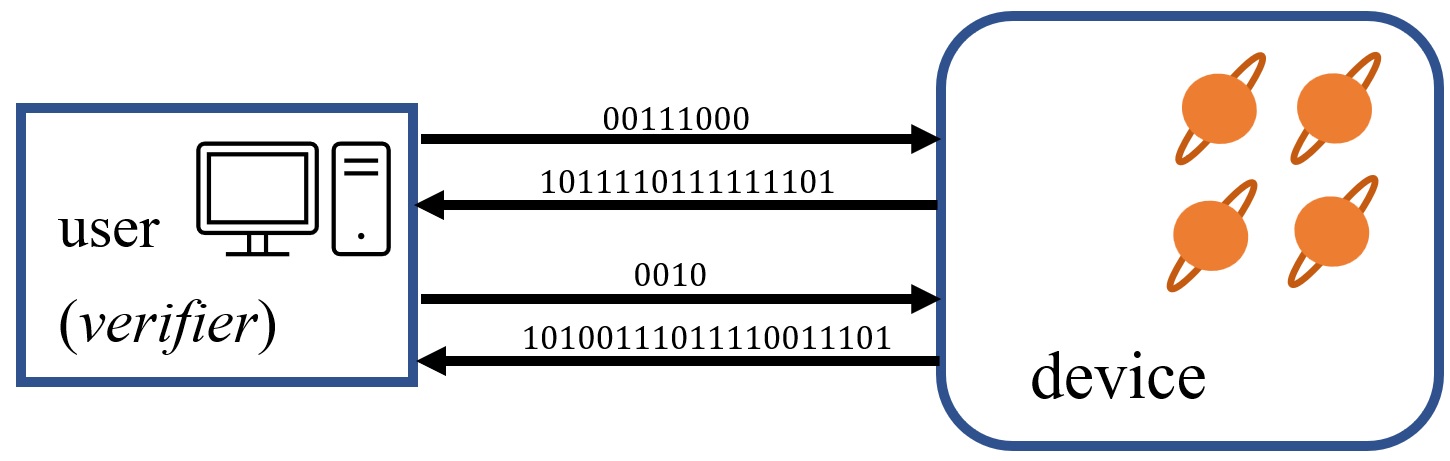
An interactive verification protocol
The design of a test of quantumness exhibits a clear tension between hardness of simulation (the task should not be solvable by a classical computer) and ease of verification (it should be possible to efficiently verify that the task has been solved). Beyond tests of quantumness it is essential to develop more informative tests that verify that the device is accomplishing a useful task, such as generating cryptographically secure outputs or correctly implementing a quantum algorithm.
Further reading
In a 2018 paper, with Brakerski and collaborators we opened a line of works that tackle these questions by using a post-quantum cryptographic assumption to gain leverage on the quantum device. In that paper we gave a test of quantumness, as well as a certifiable randomness protocol (see our related work on device-independent cryptography). Subsequently with Gheorghiu we showed that the same skeleton could lead to a qubit delegation protocol, thereby giving a slightly different approach to classical delegation of quantum computation, a problem that had been solved earlier by Mahadev in her seminal work. I later wrote an introduction to this work for the Bulletin of the AMS, which may be more digestible for readers with a background in mathematics. With Zhang we studied the zero-knowledge and proof of knowledge properties of this protocol, and with Ma and collaborators we made it succinct.