In an interactive proof, an entity with limited computational power (the verifier) interacts with one or more computationally powerful entities (referred to as the prover(s)) in an attempt to verify the validity of a certain publicly known statement -- for example, that a given integer is prime, or that a given graph admits a proper coloring. In a proof system we generally assume that the goal of the prover(s) is to make the verifier accept the statement, whereas the goal of the verifier is to make sure that they accept only true statements. Can a bounded verifier validate complex statements, that they cannot decide by themselves?
The widely held conjecture that there exists languages in NP that are not in P suggests that the answer to this basic question is yes. Yes, but how, when, and why? Over the years interactive proof systems have provided a framework in which to examine a wide range of questions, from the philosophical (e.g. which statements have verifiable proofs?) to the practical (e.g. how efficiently can a large computation be verified?). The landmark results in this area are the equalities IP = PSPACE and MIP = NEXP which characterize the collections of languages that have single-prover (IP) and multi-prover (MIP) interactive proofs as equal to the class of problems that can be solved in polynomial space (and possibly exponential time) and non-deterministic exponential time respectively. These results have had rippling consequencs throughout complexity theory and cryptography, from the design of zero-knowledge protocols to the PCP theorem and results in hardness of approximation through efficient schemes for delegated computation and formal language verification.
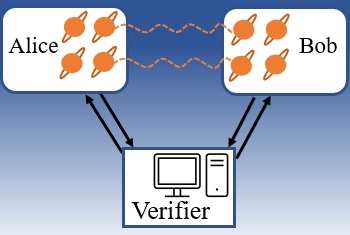
An MIP* interactive proof system
My research focuses on quantum analogues of the classes IP and MIP. These extensions are motivated by fundamental questions about the power of quantum computation (can quantum communication support more efficient verification?) and physics (can complex entanglement patterns be tested based on classical statistics?) as well as applications (can quantum computations be verified?). In a sequence of works, together with collaborators we have characterized the complexity of the class MIP*. In this class the verifier and communication are classical and polynomially bounded; the only modification compared to MIP is that the provers are allowed to share quantum entanglement. In first approximation entanglement can be thought of as a distributed resource, akin to but more powerful than shared randomness — understanding exactly how much more powerful is one of the main motivations behind the introduction of MIP*.
Further reading
For a brief, high-level introduction I can suggest the notes associated with a winter school lecture I gave on the topic. A detailed introduction to quantum (interactive) proof classes is in the small book I co-wrote with John Watrous. For technical work around MIP*, see the introduction to the MIP*=RE paper and references therein. A key technical ingredient in the proof is the quantum low-degree test, which has a complex history: see the latest paper for details.