Basic principles of quantum information such as the no-cloning principle and uncertainty relations make quantum information a facinating playing ground for cryptography. Each of these physical principles immediately suggests a success story, such as quantum money or quantum key distribution. However, they also create a difficulty: principles that place limits on the capabilities of a quantum adversary also restrict the ability of a honest user to control their quantum system.
To take a concrete example from my research, let's consider the problem of certifiable randomness. It is well-known that a simple deterministic quantum circuit can generate a perfectly uniform random bit. (Indeed “quantum random number generators” (QRNG) are one of the first commercial applications of quantum devices.) Wearing our cryptographer’s hat, we may ask, how does one know that the outcome of the QRNG is random? Certainly one needs to believe the laws of quantum mechanics. But one also needs to trust the physical equipment that was used to realize the quantum circuit. This equipment is by nature quantum, and thus subject to quantum constraints such as the uncertainty principle, which limits the ability of an outside observer to gain information about the device’s state without disturbing it. Under such constraints, how can one tell if the device is generating its output as claimed?
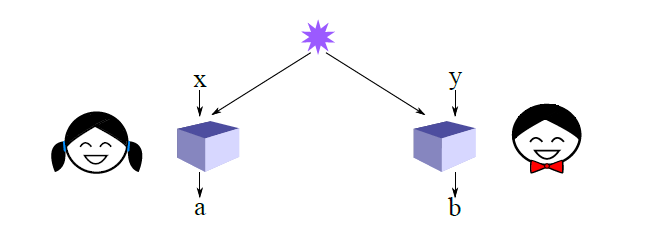
Two-player games such as the CHSH game underlie the security of device-independent cryptography.
The security notion of device independence captures this scenario, by offering security guarantees that rest on observable data only, as opposed to assumptions about
the inner workings of the quantum devices used. Beyond randomness certification the area encompasses multiple other cryptographic tasks such as quantum key distribution (QKD) as well as e.g. classical protocols for verifying quantum computations, all of which I have studied.
Further reading
For the problem of certified randomness generation, see our lightweight introduction in the Philosophical Transactions of the Royal Society A. With Vazirani we gave the first proof of security for device-independent quantum key distribution, about which we wrote an overview article in the communications of the ACM. Subsequently others found a more information-theoretic approach that leads to far better rate curves. Ideas that originate in those works eventually led to quite a range of results in complexity and cryptography; for example, see our protocol for (somewhat) efficiently delegating computations to two servers sharing entanglement, which improves on the original work of Reichardt et al.