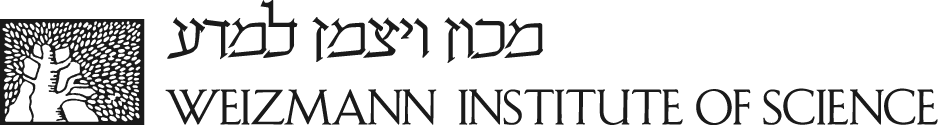Wearable & Portable Green Platforms
Developing energy-efficient signal acquisition and processing hardware is key to advancing environmental sustainability in modern Information Processing Systems (IPSs). Our lab designs novel signal processing tools and hardware architectures that significantly reduce sampling and quantization rates, dynamic range, and overall power consumption. Analog-to-Digital Converters (ADCs) are central to this effort, and our approach rethinks their core design to align with signal structure and task requirements.
We introduce several energy-efficient ADC frameworks—Green ADCs—which combine optimized analog pre-processing with advanced recovery methods. These include:
• Time-Encoding ADCs (TEM) that eliminate the global clock by encoding time intervals between events. This enables asynchronous, event-driven sampling, significantly reducing power consumption and bit rate.
• Modulo ADCs, which overcome dynamic range limitations using modulo operations. This reduces the number of bits required per sample while enabling recovery of signals with wide dynamic range.
• Task-Based ADCs, which reduce dimensionality at the analog front-end using an application-specific combiner, followed by low-resolution scalar quantization. This minimizes unnecessary data acquisition while preserving task-relevant information.
Together, these techniques enable sub-Nyquist sampling and ultra-low-bit quantization, reducing both energy usage and data rates. We demonstrate these principles in a range of hardware prototypes applied to domains such as medical imaging, radar, and communications.
Hardware demos and source files are available at: https://www.weizmann.ac.il/math/yonina/software-hardware/hardware
Time Encoding Machine (TEM)
sampling by encoding signals as time intervals rather than amplitudes. This event-driven approach results in significant power savings and simplified hardware design. Notably, in contrast to conventional ADCs, larger signal amplitudes reduce the range of timing values, thus requiring fewer bits per sample. Combined with our robust signal reconstruction algorithms, TEM enables low-bit, low-power acquisition for a wide range of signals.
TEM hardware and demo:
https://www.weizmann.ac.il/math/yonina/software-hardware/hardware/time-encoding-machine
Images: TEM Prototype | TEM Graphic User Interface (GUI)

Unlimited Dynamic Range ADC (Modulo ADC)
When signal amplitudes exceed the dynamic range of a system, traditional ADCs clip, causing irreversible distortion. The Modulo ADC overcomes this by applying a nonlinear modulo operation before quantization, effectively folding the signal within a finite range. Our recovery algorithms then unwrap the folded signal, enabling high-accuracy reconstruction with significantly fewer bits. This results in reduced hardware complexity and energy consumption while maintaining robustness.
A recent practical implementation of modulo ADCs addresses the challenge of high-frequency components by using an analog mixer followed by a low-pass filter. This enables the use of standard ADCs while maintaining accurate modulo recovery.
Modulo ADC hardware and demo:
https://www.weizmann.ac.il/math/yonina/software-hardware/hardware/high-dynamic-range-modulo-adc
Images: Modulo ADC Prototype | Modulo ADC GUI


Images: Practical Modulo ADC Prototype


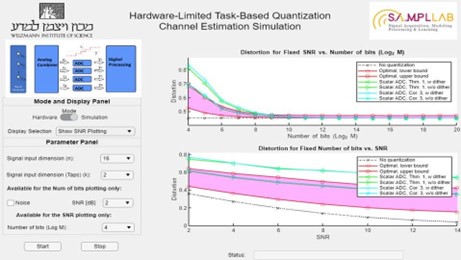
Task-Based ADC (Analog Precoder 16x4)
Most ADCs are agnostic to the task for which the signal is acquired. In contrast, our Task-Based ADCs are optimized for specific downstream applications. We employ an analog precoder that compresses the signal dimensionally before quantization, enabling accurate information extraction using a small number of low-bit scalar quantizers. This approach dramatically reduces both sampling and quantization rates, and is especially well-suited to modern high-dimensional signal acquisition.
Task-Based Quantization hardware and demo:
https://www.weizmann.ac.il/math/yonina/software-hardware/hardware

Sub-Nyquist Sampling
By exploiting signal structure, we design systems that operate well below the Nyquist rate. Our sub-Nyquist framework models signals as belonging to unions of subspaces and uses analog preprocessing (e.g., modulation, filtering, mixing) to compress the signal before sampling. We then apply compressed sensing recovery algorithms to reconstruct the signal. This principle underlies our hardware for radar, ultrasound, and cognitive radio systems.
SubNyquist Radar: We developed a real-time hardware prototype that samples radar signals at just 1/30 of the Nyquist rate using the Xampling framework. Despite the aggressive sampling reduction, the system maintains strong target detection performance, even in environments with significant noise and clutter.
https://www.weizmann.ac.il/math/yonina/software-hardware/hardware/sub-nyquist-radar-prototype
Images: Radar Prototypes | GUIs | MIMO Demo


Distorted Pulse Shape Radar: In many practical radar scenarios, the transmitted pulse shape may be unknown or distorted. Our extension uses two synchronized sub-Nyquist receivers to recover the scene without any prior knowledge of the pulse shape, maintaining the same performance as known-pulse configurations.
Images: Sub-Nyquist Radar with Distorted Pulse Shape Prototype | GUIs


MIMO Radar: We extend our sub-Nyquist methods to a collocated MIMO radar system using frequency division multiplexing (FDM). This setup reduces sampling rates across both spectral and spatial dimensions. Leveraging Xampling, we reconstruct the full scene with significantly fewer channels and lower bandwidth, making the system more scalable and energy-efficient.

Images: Cognitive Sub-Nyquist Collocated MIMO Radar Prototype
References
-
H. Naaman, N. I. Bernardo, A. Choen, and Y. C. Eldar, "Time Encoding Quantization of Bandlimited and Finite-Rate-of-Innovation Signals", IEEE Access, vol. 13, pp. 184745 - 184761, October 2025.
-
H. Naaman, S. Mulleti and Y. C. Eldar, "FRI-TEM: Time Encoding Sampling of Finite-Rate-of-Innovation Signals", IEEE Transactions on Signal Processing, vol. 70, pp. 2267-2279, April 2022.
-
E. Azar, S. Mulleti and Y. C. Eldar, "Unlimited sampling beyond modulo", Applied and Computational Harmonic Analysis, vol. 74, pp. 101715, January 2025.
-
Y. Kvich, S. Savariego, M. Namer, Y. C. Eldar, Practical Modulo Sampling: Mitigating High-Frequency Component”, arXiv preprint arXiv:2501.11330, January 2025.
-
N. Shlezinger, Y. C. Eldar and M. R. D. Rodrigues, "Hardware-Limited Task-Based Quantization", IEEE Transactions on Signal Processing, vol. 67, issue 20, pp. 5223-5238, October 2019.
-
N. Shlezinger, Y. C. Eldar and M. R. D. Rodrigues, "Asymptotic Task-Based Quantization with Application to Massive MIMO", IEEE Transactions on Signal Processing, vol. 67, issue 15, pp. 3995-4012, August 2019.
-
N. Shlezinger and Y. C. Eldar, "Task-Based Quantization with Application to MIMO Receivers", Communications in Information and Systems, vol. 20, issue 2, pp. 131-162, 2020.
-
F. Xi, N. Shlezinger, and Y. C. Eldar, "BiLiMO: Bit-Limited MIMO Radar via Task-Based Quantization", Transactions on Signal Processing, vol. 69, pp. 6267-6282, September 2021.
-
Y. C. Eldar, "Recovering Lost Information in The Digital World", SIAM News, vol. 51, issue 9, pp. 1,3, November 2018.
-
D. Cohen, S. Tsiper and Y. C. Eldar, "Analog to Digital Cognitive Radio: Sampling, Detection and Hardware", IEEE Signal Processing Magazine, vol. 35, issue 1, pp. 137-166, January 2018.
-
D. Cohen and Y. C. Eldar, "Sub-Nyquist Radar Systems: Temporal, Spectral and Spatial Compression", IEEE Signal Processing Magazine, vol. 35, issue 6, pp. 35-58, November 2018.
-
A. Kipnis, A. Goldsmith and Y. C. Eldar, "Analog-to-Digital Compression: A New Paradigm for Converting Signals to Bits", IEEE Signal Processing Magazine, vol. 35, issue 3, pp. 16-39, May 2018.