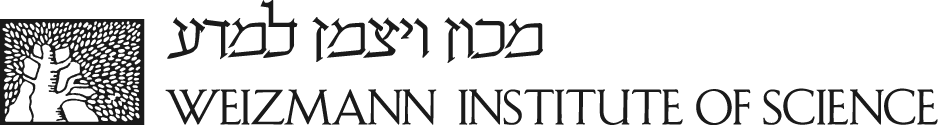Inverse Imaging for Health

Introduction

We focus on new radar (RD) and ultrasound (US) quantitative biomedical imaging algorithms and systems that are expected to quickly and accurately reconstruct the electrical and acoustic parameters of tissues and organs, realizing structural and functional imaging with high efficiency. Our solution is to develop efficient, high performance (yet interpretable), low training set reliant deep learning algorithms and network structures for RD and US quantitative imaging. In addition, specific hardware systems are built for data collection and algorithm validation.

Nonlinear US full-waveform inversion

We developed the nonlinear full waveform inversion (FWI) algorithm, which is based on representing the wave equation as an RNN, with an architecture determined by the physical acoustic model. This representation enables to apply optimization algorithms borrowed from the deep-learning toolbox and paves the way to very efficient implementation. The generality of this approach allows reconstructing multiple properties simultaneously using a nonlinear acoustics (NLA) model, which better captures the wave's propagation in the human body. 
In the Illustration of the simulated medium figure belowThis representation enables to apply optimization algorithms borrowed from the deep-learning toolb, the Water is represented in white. The left and right objects are fat and liver, respectively. The tissues and the water have different SoS, density, attenuation, and nonlinearity while the transducer array is located at the top. In the reconstruction of simulated medium figure, the first row shows the GT values of the simulated medium. The second row shows the initial values used as input to the inverse algorithm. In the third row presents the obtained reconstructions using NWI. We evaluate the difference using the normalized RMSE metric. Across all maps, white values correspond to the water's properties. The left and right objects are fat and liver respectively.  The PML layer applies a gradual attenuation, which increases close to the boundaries of the grid, as shown in the attenuation maps. 

We developed the nonlinear full waveform inversion (FWI) algorithm, which is based on representing the wave equation as an RNN, with an architecture determined by the physical acoustic model. This representation enables to apply optimization algorithms borrowed from the deep-learning toolbox and paves the way to very efficient implementation. The generality of this approach allows reconstructing multiple properties simultaneously using a nonlinear acoustics (NLA) model, which better captures the wave's propagation in the human body. In the Illustration of the simulated medium figure below, the Water is represented in white. The left and right objects are fat and liver, respectively. The tissues and the water have different SoS, density, attenuation, and nonlinearity while the transducer array is located at the top. In the reconstruction of simulated medium figure, the first row shows the GT values of the simulated medium. The second row shows the initial values used as input to the inverse algorithm. In the third row presents the obtained reconstructions using NWI. We evaluate the difference using the normalized RMSE metric. Across all maps, white values correspond to the water's properties. The left and right objects are fat and liver respectively. The PML layer applies a gradual attenuation, which increases close to the boundaries of the grid, as shown in the attenuation maps.
 

Quantitative model-based deep neural network for US and RD imaging

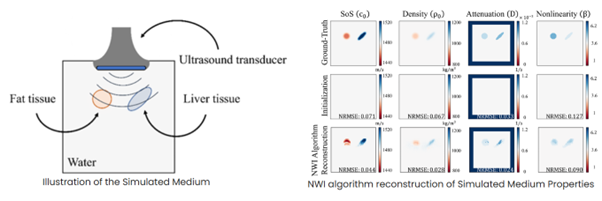
We introduce MB-QRUS, which stands for Model-Based Quantitative Radar and US, which is based on an unfolding mechanism of with learned gradients according to a U-Net based block. We use the residuals between the measured channel data and the predicted channel data, according to physical property estimation and the physical model of wave propagation, to learn the gradients which are often used to update the physical properties estimation. We also introduce a new time-domain and tensor representation of the input measured channel which captures the spatial representation of the channel data.

/math/yonina/sites/math.yonina/files/Picture1_7.png

/math/yonina/sites/math.yonina/files/Picture1_8.png

We further proposed DUFWI, deep unfolding-based approach for FWI, for quantitative US imaging. To meet the computational demands of our time-domain method, we adopt block-by-block training, allowing for the reuse of computed gradients in each epoch. This method efficiently trains the deep neural network at each iteration of the deep unfolded algorithm, enabling the use of larger simulated domains during training—a key requirement for real-world applications. Both simulation and hardware experiments on the training dataset and out-of-distribution examples show that our method outperforms classical FWI and MB-QRUS in reconstruction quality under noisy conditions while maintaining a high level of efficiency.

 

Quantitave RD imaging with generative models

We propose L-DPnP, latent diffusion plug-and-play method, for quantitative microwave RD imaging for brain. This method samples from the posterior distribution of electrical properties given RD array measurements. It includes a data consistency sampler to generate samples consistent with the measurements, and a latent diffusion model combined with a variational auto-encoder employed as an expressive prior. Our method is validated on a two-dimensional microwave dataset simulated from heads with and without hemorrhagic or ischemic strokes, showing the smallest model misfit (0.067 vs. ≥ 0.085) and highest structure similarity index measure (SSIM) (0.936 vs. ≤0.906) compared to other existing methods.

 

Reference:

  • Shultzman, Avner, and Yonina C. Eldar. "Nonlinear waveform inversion for quantitative ultrasound." IEEE transactions on computational imaging 8 (2022): 893-904.
  • Guo, Rui, Tianyao Huang, Maokun Li, Haiyang Zhang, and Yonina C. Eldar. "Physics-embedded machine learning for electromagnetic data imaging: Examining three types of data-driven imaging methods." IEEE Signal Processing Magazine 40, no. 2 (2023): 18-31. 
  • Sharon, Tom, and Yonina C. Eldar. "Real-time model-based quantitative ultrasound and radar." IEEE Transactions on Computational Imaging (2024). 
  • Cohen, Niv, Yhonatan Kvich, Rui Guo, and Yonina C. Eldar. "Deep Unfolding of Full Waveform Inversion for Quantitative Ultrasound Imaging." In ICASSP 2025-2025 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 1-5. IEEE, 2025. 
  • Guo, Rui, Yhonatan Kvich, Yi Zhang, Tianyao Huang, Maokun Li, and Yonina C. Eldar. "Posterior Sampling with Latent Diffusion for Microwave Brain Imaging." In 2025 47th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), pp. 1-7. IEEE, 2025. 
  • Guo, Rui, Yi Zhang, Yhonatan Kvich, Tianyao Huang, Maokun Li, and Yonina C. Eldar., Plug-and-Play Latent Diffusion for Electromagnetic Inverse Scattering with Application to Brain Imaging (https://arxiv.org/pdf/2509.04860).