Generative, Physics-informed AI

Background:

signal processing, communications, and control have traditionally relied on classical statistical modeling techniques. Such model-based methods utilize mathematical formulations that represent the underlying physics, prior information, and additional domain knowledge. Simple classical models are useful but sensitive to inaccuracies and may lead to poor performance when real systems display complex or dynamic behavior. On the other hand, purely data-driven deep learning approaches that are model-agnostic are becoming increasingly popular, which use generic architectures such as deep neural networks (DNNs) that learn to operate from data and demonstrate excellent performance, especially for supervised problems. However, DNNs typically require massive amounts of data and immense computational resources, limiting their applicability for some scenarios.

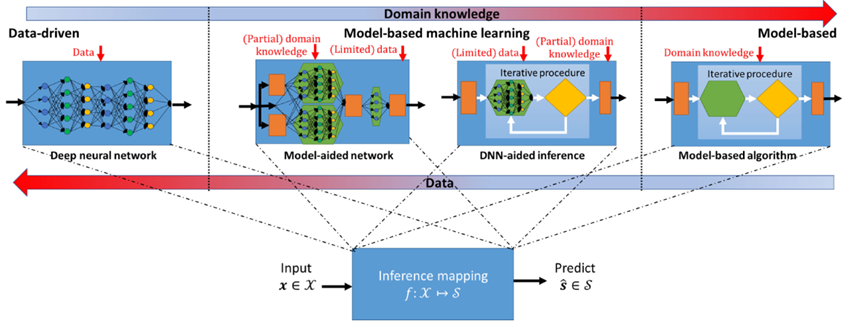
                                                                                          Fig. 1 Illustration of model-based versus data-driven inference.

 

In our lab, we are working on model-based deep learning methods that combine principled mathematical models with data-driven systems to benefit from the advantages of both approaches. Such model-based deep learning methods exploit both partial domain knowledge, via mathematical structures designed for specific problems, and learning from limited data. Our goal is to facilitate the design, application and theoretical study of future model-based deep learning algorithms at the intersection of signal processing and machine learning.

The software can be found at: https://www.weizmann.ac.il/math/yonina/software-hardware/software

Methods:

Here we introduce two major strategies for model-based deep learning: The first category includes DNNs whose architecture is specialized to the specific problem using model-based methods, referred to here as model-aided networks. The second one, which we refer to as DNN-aided inference, consists of techniques in which inference is carried out by a model-based algorithm whose operation is augmented with deep learning tools.

Model-Aided Networks:

Model-aided networks implement model-based deep learning by using model-aware algorithms to design deep architectures. Broadly speaking, model-aided networks implement the inference system using a DNN, similar to conventional deep learning. Nonetheless, instead of applying generic off-the-shelf DNNs, the rationale here is to tailor the architecture specifically for the scenario of interest, based on a suitable model-based method. By converting a model-based algorithm into a model-aided network, which learns its mapping from data, one typically achieves improved inference speed, as well as overcome partial or mismatched domain knowledge.  Specifically, we are interested in an import class of model-aided networks termed unfolded/unrolled networks. The corresponding technique for designing deep architectures,  termed algorithm unfolding/unrolling, converts an iterative algorithm into a DNN by designing each layer to resemble a single iteration (see Fig. 2). In this direction, we are developing more powerful architecture of unrolling algorithms for a wider variety of tasks (see Fig. 3 for an example), from super-resolution in optical microscopy and ultrasound to speed-of-sound reconstruction using ultrasonography, to the development of modern wireless systems, to image deblurring, signal separation, and more.

         

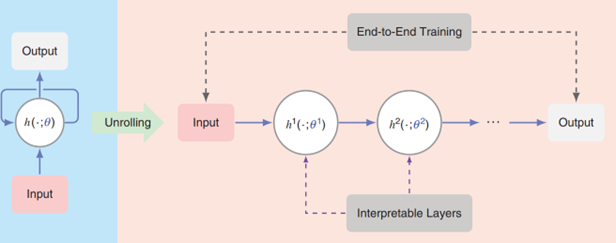
Fig. 2 A high-level overview of algorithm unrolling. The original iterative algorithm repeatedly applies a parametric mapping h(⋅;θ) to update the iterate, where θ is a hyperparameter that comes from the algorithmic setting (e.g., stepsize of a gradient descent algorithm) or the problem of interest (e.g., measurement matrix in a linear inverse problem). By unrolling, we design a neural network with each layer having the same structure as h(⋅;θ) and treat θ  therein as a learnable parameter. Given a dataset of paired input and output, we can optimize θ in each layer via standard deep learning techniques, thereby obtaining an interpretable deep neural network.

     

 

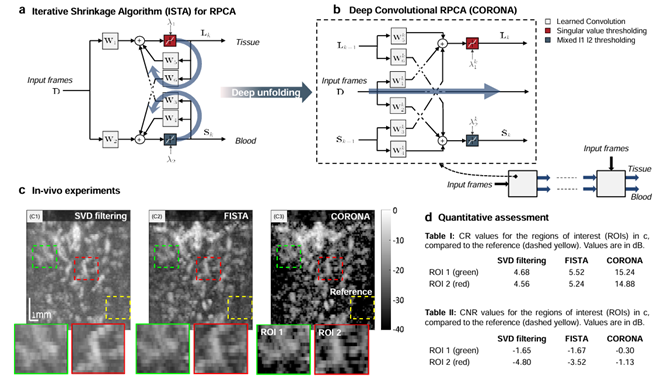
Fig. 3 CORONA: a deep unfolded robust PCA algorithm with application to clutter suppresion in ultrasound. Details, source code and data can be found at: Deep Unfolded Robust PCA with Application to Ultrasound Imaging | Yonina Eldar

 

Fig. 4 Learned SPARCOM: unfolded deep super-resolution microscopy. Details, source code and data can be found at: Learned SPARCOM:Unfolded Deep Super-Resolution Microscopy | Yonina Eldar

 

Fig. 5 Deep unfolding of ultrasound full waveform inversion.

DNN-Aided Inference:

DNN-aided inference is a family of model-based deep learning algorithms in which DNNs are incorporated into model-based methods. As opposed to model-aided networks, where the resultant system is a deep network whose architecture imitates the operation of a model-based algorithm, here, the inference is carried out using a traditional model-based method, while some of the intermediate computations are augmented by DNNs so as to mitigate sensitivity to inaccurate model knowledge, facilitate operation in complex environments, and enable application in new domains. The following demo movie introduces ViterbiNet, which is a DNN-aided Viterbi algorithm for symbol detection (i.e., recovering a message transmitted by a remote transmitter through a noisy channel).

         

Fig. 6 DNN-aided factor graph methods. Details can be found at: Learned Factor Graphs for Inference From Stationary Time Sequences

Fig. 7 Classic Kalman filter (left) vs. DNN-aided Kalman filter (right). Details can be found at: KalmanNet: Neural Network Aided Kalman Filtering for Partially Known Dynamics

Theory:

Despite great success of deep learning, to establish a solid mathematical theory to facilitate the understanding of DNNs and to guide the use of deep learning tools still remains an important challenge. In contrast to standard deep learning pipelines, model-based deep learning algorithms incorporate domain knowledge in the network architecture and training objective, providing additional support to derive theoretical guarantees of the algorithms. Our group is also active in theoretical studies of model-based DNNs, aiming to develop a theoretical understanding of the advantage of model-based DNNs over standard DNNs; see [12-14] for examples.

 

References:

[1] V. Monga, Y. Li, and Y. C. Eldar, "Algorithm Unrolling: Interpretable, Efficient Deep Learning for Signal and Image Processing", IEEE Signal Processing Magazine, vol. 38, issue 2, pp. 18-44, March 2021.

[2] N. Shlezinger, Y. C. Eldar, and S. P. Boyd, "Model-Based Deep Learning: On the Intersection of Deep Learning and Optimization", IEEE Access, vol. 10, pp. 115384-115398, November 2022.

[3] N. Shlezinger, J. Whang, Y. C. Eldar and A. G. Dimakis, "Model-Based Deep Learning", Proceedings of the IEEE, vol. 111 (5), pp. 465-499, May 2023.

[4] N. Shlezinger and Y. C. Eldar, "Model-Based Deep Learning", Foundations and Trends in Signal Processing, Vol. 17 (4), pp 291-416, August 2023.

[5] Y. Ben Sahel, J. P. Bryan, B. Cleary, S. L. Farhi and Y. C. Eldar, "Deep Unrolled Recovery in Sparse Biological Imaging", IEEE Signal Processing Magazine, vol. 39 (2), pp. 457-57,  February 2022.

[6] N. Farsad, N. Shlezinger, A. J. Goldsmith, and Y. C. Eldar,  "Data-Driven Symbol Detection via Model-Based Machine Learning", Communications in Information and Systems, vol. 20, issue 3, pp. 283–317, 2020.

[7] G. Dardikman-Yoffe and Y. C. Eldar, "Learned SPARCOM: Unfolded Deep Super-Resolution Microscopy", Optics Express, vol. 28, issue 19, pp. 27736-27763, September 2020.

[8] O. Bar-Shira, A. Grubstein, Y. Rapson, D. Suhami, E. Atar , K. Peri-Hanania, R. Rosen ,Y. C. Eldar, "Learned Super Resolution Ultrasound for Improved Breast Lesion Characterization", MICCAI 2021.

[9] O. Solomon, R. Cohen, Y. Zhang, Y. Yang, H. Qiong, J. Luo, R. J. G. van Sloun and Y. C. Eldar, "Deep Unfolded Robust PCA with Application to Clutter Suppression in Ultrasound", vol. 39, issue 4, pp. 1051-1063, IEEE Transactions on Medical Imaging, April 2020.

[10] N. Shlezinger, N. Farsad, Y. C. Eldar, and A. J. Goldsmith, "ViterbiNet: Symbol Detection Using a Deep Learning Based Viterbi Algorithm", IEEE Transactions on Wireless Communications, vol. 19, issue 5, pp. 3319-3331, May 2020.

[11] G. Revach, N. Shlezinger, X. Ni, A. L. Escoriza, R. J. G. van Sloun and Y. C. Eldar, "KalmanNet: Neural Network Aided Kalman Filtering for Partially Known Dynamics", in IEEE Transactions on Signal Processing, vol. 70, pp. 1532-1547, March 2022.

[12] A. Shultzman, E. Azar, M. Rodrigues and Y. C. Eldar, "Generalization and Estimation Bounds for Model-based Neural Networks", ICLR, May 2023.

[13] S. B. Shah, P. Pradhan, W. Pu, R. Randhi, M. R. D. Rodrigues and Y. C. Eldar, "Optimization Guarantees of Unfolded ISTA and ADMM Networks With Smooth Soft Thresholding", IEEE Transactions on Signal Processing, vol. 72, pp. 3272-3286, May 2024.

[14] A. Karan, K. Shah, S. Chen, and Y. C. Eldar, “Unrolled denoising networks provably learn optimal Bayesian inference,” Advances in Neural Information Processing Systems, 2024.